Unterschied zwischen Binomial und Normalverteilung

Binomial gegen Normalverteilung
 

Wahrscheinlichkeitsverteilungen von Zufallsvariablen spielen eine wichtige Rolle im Bereich der Statistik. Aus diesen Wahrscheinlichkeitsverteilungen sind Binomialverteilung und Normalverteilung zwei der am häufigsten vorkommenden im wirklichen Leben.

Was ist Binomialverteilung?

Die Binomialverteilung ist die Wahrscheinlichkeitsverteilung, die der Zufallsvariablen entspricht X, Welches ist die Anzahl der Erfolge von a endliche Sequenz von unabhängigen Ja/Nein -Experimenten jeweils eine Erfolgswahrscheinlichkeit P. Aus der Definition von X, Es ist offensichtlich, dass es sich um eine diskrete Zufallsvariable handelt. Daher ist die Binomialverteilung auch diskret.

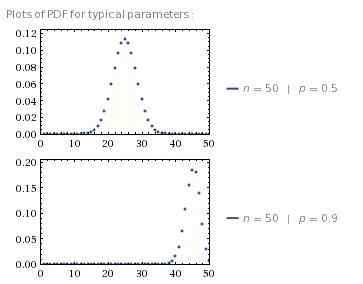
Die Verteilung wird als bezeichnet als X ~B(N,P) Wo N ist die Anzahl der Experimente und P ist die Erfolgswahrscheinlichkeit. Nach der Wahrscheinlichkeitstheorie können wir das ableiten B(N,P) folgt der Wahrscheinlichkeitsmassenfunktion [Latex] b (n, p) \\ Sim \\ binom n k p^k (1-p)^(n-k), k = 0, 1, 2,… n [/Latex]. Aus dieser Gleichung kann weiter abgeleitet werden, dass der erwartete Wert von X, E (X) = np und die Varianz von X, V (X) = np(1-P).

Betrachten Sie beispielsweise ein zufälliges Experiment, wie Sie eine Münze dreimal geworfen haben. Definieren Sie den Erfolg als Erhalt von H, Versagen als Erhalt von T und die Zufallsvariable X als Anzahl der Erfolge im Experiment. Dann X~B(3, 0.5) und die Wahrscheinlichkeitsmassenfunktion von X gegeben durch [Latex] \\ binom 3 k 0.5^k (0.5)^(3-k), k = 0, 1, 2.[/Latex]. Daher ist die Wahrscheinlichkeit, mindestens 2 h zu erhalten, P (X ≥ 2) = P (X = 2 oder X = 3) = P (X = 2) + p (X = 3) = ³C₂(0.5²) (0.5¹) + ³C₃(0.5³) (0.5⁰) = 0.375 + 0.125 = 0.5.

Was ist Normalverteilung?

Normalverteilung ist die durch die Wahrscheinlichkeitsdichtefunktion definierte Wahrscheinlichkeitsverteilung [Latex] n (\\ mu, \\ sigma) \\ Sim \\ Frac 1 \\ SQRT 2 \\ Pi \\ Sigma^ 2 \\ e^- \\ frac (x- \\ mu)^2 2 \\ sigma^2 [/latex]. Die Parameter [Latex] \\ mu und \\ sigma [/latex] bezeichnen den Mittelwert und die Standardabweichung der interessierenden Bevölkerung. Wenn [Latex] \\ mu = 0 und \\ sigma = 1 [/latex] die Verteilung als Standardnormalverteilung bezeichnet wird.

Diese Verteilung wird als normal bezeichnet, da die meisten natürlichen Phänomene der Normalverteilung folgen. Beispiel wird der IQ der menschlichen Bevölkerung normal verteilt. Wie aus der Grafik aus erscheint, ist es unimodal, symmetrisch über den Mittelwert und die glockenförmige Form. Der Mittelwert, der Modus und der Median fällt zusammen. Die Fläche unter der Kurve entspricht dem Teil der Bevölkerung und erfüllt einen bestimmten Zustand.

Die Teile der Bevölkerung im Intervall [Latex] (\\ mu - \\ sigma, \\ mu + \\ sigma) [/latex], [latex] (\\ mu - 2 \\ sigma, \\ mu + 2 \\ sigma) [/latex], [latex] (\\ mu - 3 \\ sigma, \\ mu + 3 \\ sigma) [/latex] sind ungefähr 68.2%, 95.6% und 99.8%.

Was ist der Unterschied zwischen Binomial- und Normalverteilungen?

• Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung, während die Normalverteilung eine kontinuierliche ist.
• Die Wahrscheinlichkeitsmassenfunktion der Binomialverteilung lautet [Latex] B (n, p) \\ Sim \\ binom n k p^k (1-p)^(n-k) [/latex] Während die Wahrscheinlichkeitsdichtefunktion der Normalverteilung [Latex] n (\\ mu, \\ sigma) \\ Sim \\ Frac 1 \\ SQRT 2 \\ pi \\ sigma^2 ist, lautet \\ e^- \\ frac (x- \\ mu)^2 2 \\ sigma^2 [/latex]
• Die binomiale Verteilung wird unter bestimmten Bedingungen mit der Normalverteilung angenähert, jedoch nicht umgekehrt.