Unterschied zwischen Umfang, Incenter, Orthocenter und Schwerpunkt

Umfang, Incenter, Orthocenter gegen Zentroid

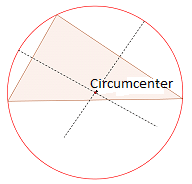
Umfang: Umfang ist der Schnittpunkt von drei senkrechte Bisektoren eines Dreiecks. Umfang ist das Zentrum der Umkreis, Das ist ein Kreis, der durch alle drei Eckpunkte eines Dreiecks verläuft.

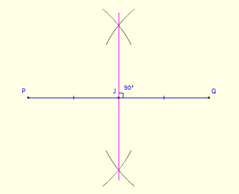
Zum Zeichnen des Umgebungsnutzers zwei beliebige senkrechte Bisektoren an den Seiten des Dreiecks erstellen. Der Schnittpunkt gibt das Umfangscenter. Mit dem Kompass und der geraden Kante des Herrschers kann ein Halbierende erstellt werden. Stellen Sie den Kompass auf einen Radius ein, der mehr als die Hälfte der Länge des Liniensegments entspricht. Machen Sie dann zwei Bögen auf beiden Seiten des Segments mit einem Ende als Zentrum des Bogens. Wiederholen Sie den Vorgang mit dem anderen Ende des Segments. Die vier Bögen erzeugen zwei Schnittpunkte auf beiden Seiten des Segments. Zeichnen Sie eine Linie, die diese beiden Punkte mit Hilfe des Herrschers verbindet, und das wird die senkrechte Halbierende des Segments verleihen.

Um den Zähler zu erzeugen, zeichnen Sie einen Kreis mit dem Umfang als Zentrum und der Länge zwischen dem Umfang und einem Scheitelpunkt als Radius des Kreises.

Im zentrum: Anreiz ist der Schnittpunkt der drei WinkelhalbierendeS. Anreiz ist die Mitte des Kreises mit dem Umfang alle drei Seiten des Dreiecks kreuzen.

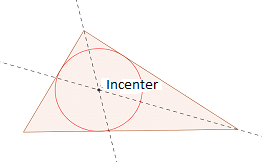
Um den Anreiz eines Dreiecks zu zeichnen, erstellen Sie zwei interne interne Winkel Halbiersektoren des Dreiecks. Der Schnittpunkt der beiden Winkelbisektoren gibt den Anreiz. Um den Winkelhaltender zu zeichnen, machen Sie zwei Bögen auf jedem der Arme mit dem gleichen Radius. Dies liefert zwei Punkte (eines an jedem Arm) am Winkelarme der Arme. Zeichnen Sie dann jeden Punkt auf den Armen als Zentren, zeichnen Sie zwei weitere Bögen. Der durch den Schnittpunkt dieser beiden Bögen konstruierte Punkt ergibt einen dritten Punkt. Eine Linie, die den Scheitelpunkt des Winkels und der dritte Punkt verbindet.

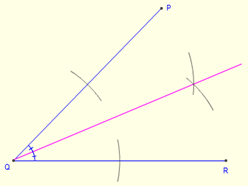
Um das zu erstellen Incircle, Konstruieren Sie ein Liniensegment senkrecht zu einer Seite, die durch den Anreiz verläuft. Zeichnen Sie die Länge zwischen der Basis des senkrechten und des Anreiz. 

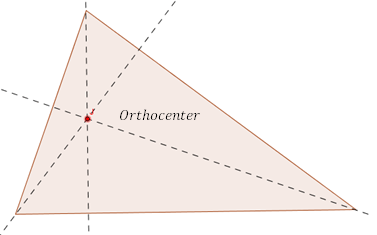
Orthocenter: Orthocenter ist der Schnittpunkt der drei Höhen (Höhen) des Dreiecks.

Um das Orthocenter zu erstellen, zeichnen Sie zwei Zweie Höhen eines Dreiecks. Ein Liniensegment senkrecht zu einer Seite, die durch den gegnerischen Scheitelpunkt fließt, wird als Höhe bezeichnet. Um eine senkrechte Linie zu zeichnen, die durch einen Punkt verläuft, markieren Sie zunächst zwei Bögen auf der Linie mit dem Punkt als Zentrum. Erstellen Sie dann zwei weitere Bögen mit jedem der Schnittpunkte als Zentrum. Zeichnen Sie ein Liniensegment, das den ersten Punkt und den schließlich konstruierten Punkt verbindet, und das verleiht die Linie senkrecht zum Liniensegment und verläuft den ersten Punkt durch den ersten Punkt. Der Schnittpunkt der beiden Höhen gibt dem Orthocenter.

Schwerpunkt: Centroid ist der Schnittpunkt der drei Median eines Dreiecks. Zentroid teilt jeden Median im Verhältnis 1: 2 auf.

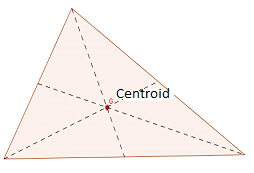
Um das Schwerpunkt zu bestimmen, erstellen Sie zwei beliebige Mediane des Dreiecks. Markieren Sie zum Erstellen eines Medians den Mittelpunkt einer Seite. Erstellen Sie dann ein Liniensegment, das den Mittelpunkt und den gegnerischen Scheitelpunkt des Dreiecks verbindet. Der Schnittpunkt der Medianer gibt den Schwerpunkt eines Dreiecks.

Was sind die Unterschiede zwischen Umfang, Incenter, Orthocenter und Zentroid?

• Umfangcenter wird unter Verwendung der senkrechten Halbierende des Dreiecks erstellt.

• Anreize werden unter Verwendung der Winkel Bisektoren der Dreiecke erstellt.

• Orthocenter wird unter Verwendung der Höhen (Höhen) des Dreiecks erstellt.

• Zentroid wird mit den Medianen des Dreiecks erstellt.

• Sowohl das Umfang als auch der Anreiz haben Kreise mit spezifischen geometrischen Eigenschaften assoziiert.

• Centroid ist das geometrisches Zentrum des Dreiecks, und es ist das Massenzentrum eines einheitlichen dreieckigen Laminars.

• Für ein nicht gleichseitiges Dreieck, das Umfang, Orthocenter und das Schwerpunkt liegen auf einer geraden Linie, und die Linie ist als die bekannt Euler -Linie.