Unterschied zwischen Umfang, Durchmesser und Radius

Umfang vs Durchmesser gegen Radius
 

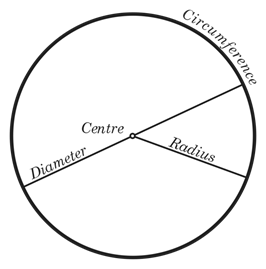
Radius, Durchmesser und Umfang sind Messungen von drei wichtigen Eigenschaften eines Kreises.

Durchmesser und Radius

Ein Kreis ist definiert als der Ort eines Punktes in einem konstanten Abstand von einem Fixpunkt auf einer zweidimensionalen Ebene. Der Fixpunkt ist als Zentrum bekannt. Die konstante Länge ist als Radius bekannt. Es ist der kürzeste Abstand zwischen der Mitte und dem Ort. Ein Liniensegment, das vom Ort beginnt, der durch die Mitte und endet am Ort, wird als Durchmesser bezeichnet.

Der Radius und der Durchmesser sind wichtige Parameter eines Kreises, da sie die Größe des Kreises bestimmen. Um einen Kreis zu zeichnen, ist nur Radius oder Durchmesser erforderlich.

Durchmesser und Radius werden mathematisch durch die folgende Formel verwandt

D = 2R

Wo D ist das dIMMETER UND r ist das Radius.

Umfang

Der Ort des Punktes ist als Umfang bekannt. Der Umfang ist eine gekrümmte Linie, und ihre Länge hängt vom Radius oder dem Durchmesser ab. Die mathematische Beziehung zwischen Radius (oder Durchmesser) und dem Umfang wird durch die folgende Formel angegeben:

C = 2πr = πd

Wo C ist der Umfang und π = 3.14. Der griechische Brief Pi (π) ist in vielen mathematischen und physikalischen Systemen konstant und wichtig. Es ist eine irrationale Zahl und hat den Wert 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… In den meisten Fällen der Wert von PI bis zwei Dezimalplätze, M -Dekimalplätze, M -Dekimalplätze, M -Dekimalplätze, M.e. π = 3.14 ist ausreichend für eine beträchtliche Genauigkeit.

Oft wird die obere Formel in der Schulmathematik in mittlerer Ebene verwendet, um die Konstante zu definieren Pi (π) als Verhältnis zwischen dem Durchmesser eines Kreises und seinem Umfang, wobei sein Wert ungefähr als Bruch 22/7 angegeben ist.

Was ist der Unterschied zwischen Umfang, Radius und Durchmesser?

• Radius und Durchmesser sind gerade Linien, während der Umfang eine geschlossene Kurve ist.

• Der Durchmesser ist doppelt so hoch wie der Radius.

• Der Umfang ist das 2π -mal der Radius des Kreises oder π -mal den Durchmesser des Kreises.