Unterschied zwischen gerichteter und ungerichteter Graphen

Regie gegen ungerichtete Graphen

Ein Diagramm ist eine mathematische Struktur, die aus Scheitelpunkten und Kanten besteht. Ein Diagramm repräsentiert eine Reihe von Objekten (dargestellt durch Scheitelpunkte), die durch einige Links (dargestellt durch Kanten) verbunden sind). Unter Verwendung mathematischer Notationen kann ein Diagramm durch g dargestellt werden, wobei g = (v, e) und v der Satz von Scheitelpunkten und e der Satz von Kanten ist. In einem ungerichteten Diagramm gibt es keine Richtung mit den Kanten, die die Scheitelpunkte verbinden. In einem gerichteten Diagramm gibt es eine Richtung, die den Kanten zugeordnet ist, die die Scheitelpunkte verbinden.

Ungerichtete Grafik

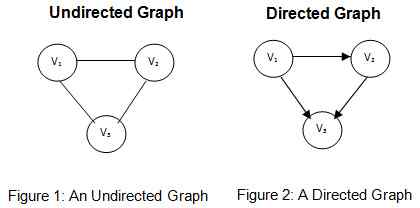
Wie bereits erwähnt, ist ein ungerichteter Diagramm ein Diagramm, in dem in den Kanten keine Richtung vorhanden ist. Abbildung 1 zeigt einen ungerichteten Graphen mit Satz von Scheitelpunkten v = v1, v2, v3. Der Satz von Kanten im obigen Diagramm kann als v = (v1, v2), (v2, v3), (v1, v3) geschrieben werden. Es ist auch zu beachten. Daher sind Kanten in einem ungerichteten Diagramm keine geordneten Paare. Dies ist das Hauptmerkmal einer ungerichteten Grafik. Unbekannte Diagramme können verwendet werden, um symmetrische Beziehungen zwischen Objekten darzustellen, die durch Scheitelpunkte dargestellt werden. Beispielsweise kann ein Zwei -Wege -Straßennetzwerk, das eine Reihe von Städten verbindet. Die Städte können durch die Eckpunkte im Diagramm dargestellt werden und die Kanten repräsentieren die zwei Wege Straßen, die die Städte verbinden.

Gerichteter Graph

Ein gerichteter Diagramm ist ein Diagramm, in dem die Kanten in der Grafik, die die Scheitelpunkte verknüpfen. Abbildung 2 zeigt einen gerichteten Diagramm mit den Eckpunkten v = v1, v2, v3. Der Satz von Kanten im obigen Diagramm kann als v = (v1, v2), (v2, v3), (v1, v3) geschrieben werden. Kanten in einem ungerichteten Diagramm sind geordnete Paare. Formal kann die Kante E in einem gerichteten Diagramm durch das geordnete Paar e = (x, y) dargestellt werden , Beenden von Scheitelpunkten oder Terminalpunkten. Beispielsweise kann ein Straßennetzwerk, das eine Reihe von Städten mit einem Weg mit einer Wege verbindet, mithilfe eines ungerichteten Diagramms dargestellt werden. Die Städte können durch die Scheitelpunkte im Diagramm dargestellt werden, und die gerichteten Kanten repräsentieren die Straßen, die die Städte anschließen, unter Berücksichtigung der Richtung, in die der Verkehr auf der Straße fließt.

Was ist der Unterschied zwischen gerichteten Graphen und ungerichteten Graphen?

In einem gerichteten Diagramm ist eine Kante ein geordnetes Paar, in dem das geordnete Paar die Richtung der Kante darstellt, die die beiden Scheitelpunkte verbindet. Andererseits ist eine Kante in einem ungerichteten Diagramm ein ungeordnetes Paar, da mit einer Kante keine Richtung zugeordnet ist. Unbekannte Diagramme können verwendet werden, um symmetrische Beziehungen zwischen Objekten darzustellen. In-Grad und Outdo-Grad jedes Knotens in einem ungerichteten Diagramm ist gleich, aber dies gilt nicht für eine gerichtete Grafik. Bei Verwendung einer Matrix zur Darstellung eines ungerichteten Diagramms wird die Matrix immer zu einem symmetrischen Graphen, dies gilt jedoch nicht für gerichtete Diagramme. Ein ungerichteter Diagramm kann in einen gerichteten Diagramm umgewandelt werden, indem jede Kante durch zwei gerichtete Kanten in entgegengesetzte Richtung ersetzt wird. Es ist jedoch nicht möglich, ein gerichtetes Diagramm in ein ungerichteter Diagramm umzuwandeln.