Unterschied zwischen Laplace und Fourier -Transformationen

Laplace gegen Fourier -Transformationen
 

Sowohl Laplace -Transformation als auch Fourier -Transformation sind integrale Transformationen, die am häufigsten als mathematische Methoden zur Lösung mathematisch modellierter physikalischer Systeme verwendet werden. Der Prozess ist einfach. Ein komplexes mathematisches Modell wird unter Verwendung einer integralen Transformation in ein einfacheres, lösbares Modell konvertiert. Sobald das einfachere Modell gelöst ist, wird die inverse integrale Transformation angewendet, die die Lösung für das Originalmodell liefert.

Da die meisten physikalischen Systeme beispielsweise zu Differentialgleichungen führen, können sie in algebraischen Gleichungen oder zu leicht lösbaren Differentialgleichungen mit einer integrierten Transformation umgewandelt werden. Dann wird die Lösung des Problems einfacher.

Was ist die Laplace -Transformation?

Bei einer Funktion F (T) einer echten Variablen T, Die Laplace-Transformation wird durch das integrale [latex] f (s) = \\ int_ 0^\\ infty e^-st f (t) dt [/latex] definiert (wann immer es existiert), welche ist eine Funktion einer komplexen Variablen S. Es wird normalerweise mit L bezeichnetF (T). Die inverse Laplace -Transformation einer Funktion F(S) wird als die Funktion angesehen F (T) so, dass L F (T) = F(S) und in der üblichen mathematischen Notation, die wir schreiben, l ^-1F(S) = F (T).Die inverse Transformation kann einzigartig gemacht werden, wenn Nullfunktionen nicht zulässig sind. Man kann diese beiden als lineare Operatoren identifizieren, die im Funktionsraum definiert sind, und es ist auch leicht zu erkennen, dass L ^-1L F (T) = F (T), wenn Nullfunktionen nicht zulässig sind.

In der folgenden Tabelle werden die Laplace -Transformationen einiger der häufigsten Funktionen aufgeführt.

Was ist die Fourier -Transformation?

Bei einer Funktion F (T) einer echten Variablen T, seine Laplace-Transformation wird durch das integrale [latex] f (\\ alpha) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ Infty^\\ Infty definiert e^i \\ alpha t f (t) dt [/latex] (wann immer es existiert) und wird normalerweise durch f bezeichnet F (T). Die inverse Transformation f ^-1F(α) wird durch das integrale [latex] f (t) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ Infty^\\ Infty e^ -i \\ alpha t f (\\ alpha) d \\ alpha [/latex]. Die Fourier -Transformation ist ebenfalls linear und kann als Operator betrachtet werden, das im Funktionsraum definiert ist.

Mit der Fourier -Transformation kann die ursprüngliche Funktion wie folgt geschrieben werden.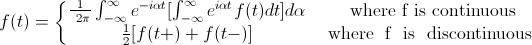

Was ist der Unterschied zwischen dem Laplace und dem Fourier -Transformationen?

• Fourier -Transformation einer Funktion F (T) ist definiert als [latex] f (\\ alpha) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ Infty^\\ infty e^i \\ alpha t f (t) dt [/latex], wohingegen die Laplace-Transformation als [latex] f (s) = \\ int_ 0^\\ Infty e^-st definiert ist f (t) dt [/latex].
• Die Fourier -Transformation wird nur für Funktionen definiert, die für alle realen Zahlen definiert sind, während die Laplace -Transformation nicht erfordert, dass die Funktion auf den festgelegten reellen Zahlen definiert wird.
• Fourier -Transformation ist ein Sonderfall der Laplace -Transformation. Es ist ersichtlich, dass beide für nicht negative reelle Zahlen übereinstimmen. (ich.e. nehmen S im Laplace zu sein Iα + β Wo α Und β sind real, so dass e ^β= ¹/_{√ (2ᴫ)})
• Jede Funktion mit einer Fourier-Transformation wird eine Laplace-Transformation haben, aber nicht umgekehrt.