Unterschied zwischen linearen und nichtlinearen Differentialgleichungen

Lineare gegen nichtlineare Differentialgleichungen
Eine Gleichung, die mindestens einen Differentialkoeffizienten oder Ableitung einer unbekannten Variablen enthält. Eine Differentialgleichung kann entweder linear oder nicht linear sein. Der Umfang dieses Artikels ist zu erklären.
Seit der Entwicklung von Kalkül im 18. Jahrhundert durch die Mathematiker wie Newton und Leibnitz hat die Differentialgleichung eine wichtige Rolle in der Geschichte der Mathematik gespielt. Differentialgleichungen sind in der Mathematik aufgrund ihres Anwendungsbereichs von großer Bedeutung. Differentialgleichungen sind im Mittelpunkt jedes Modells, das wir entwickeln, um jedes Szenario oder Ereignis der Welt zu erklären, sei es in Physik, Ingenieurwesen, Chemie, Statistik, Finanzanalyse oder Biologie (die Liste ist endlos). Tatsächlich waren bis zur etablierten Theorie die richtigen mathematischen Instrumente nicht verfügbar, um die interessanten Probleme in der Natur zu analysieren.
Die resultierenden Gleichungen aus einer spezifischen Anwendung von Kalkül können sehr komplex sein und manchmal nicht lösbar. Es gibt jedoch solche, die wir lösen können, können aber gleich aussehen und verwirrend. Für einfachere Identifizierungsdifferentialgleichungen werden daher nach ihrem mathematischen Verhalten kategorisiert. Linear und nichtlinear ist eine solche Kategorisierung. Es ist wichtig, den Unterschied zwischen linearen und nichtlinearen Differentialgleichungen zu identifizieren.
Was ist eine lineare Differentialgleichung?
Nehme an, dass f: x → y Und f (x) = y, a Differentialgleichung ohne nichtlineare Begriffe der unbekannten Funktion y und seine Derivate werden als lineare Differentialgleichung bekannt.
Es stellt die Bedingung auf, dass y höhere Indexbegriffe wie y haben kann2, y3,… Und Vielfache von Derivaten wie z
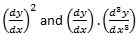
Es kann auch nicht lineare Begriffe wie die Sünde enthalten y, ey^-2, oder ln y. Es nimmt die Form an,
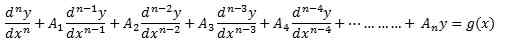
Wo y Und G sind Funktionen von X. Die Gleichung ist eine Differentialgleichung der Ordnung N, Welches ist der Index des Ableitung mit höchster Ordnung.
In einer linearen Differentialgleichung ist der Differentialoperator ein linearer Operator und die Lösungen bilden einen Vektorraum. Infolge der linearen Natur des Lösungssatzes ist eine lineare Kombination der Lösungen auch eine Lösung für die Differentialgleichung. Das heißt, wenn y1 Und y2 sind dann Lösungen der Differentialgleichung C1 y1+ C2 y2 ist auch eine Lösung.
Die Linearität der Gleichung ist nur ein Parameter der Klassifizierung und kann weiter in homogene oder nicht-homogene und gewöhnliche oder partielle Differentialgleichungen eingeteilt werden. Wenn die Funktion ist G= 0 dann ist die Gleichung eine lineare homogene Differentialgleichung. Wenn F ist eine Funktion von zwei oder mehr unabhängigen Variablen (f: x, t → y) Und f (x, t) = y , Dann ist die Gleichung eine lineare partielle Differentialgleichung.
Die Lösungsmethode für die Differentialgleichung hängt vom Typ und den Koeffizienten der Differentialgleichung ab. Der einfachste Fall entsteht, wenn die Koeffizienten konstant sind. Klassisches Beispiel für diesen Fall ist Newtons zweites Bewegungsgesetz und seine verschiedenen Anwendungen. Newtons zweites Gesetz erzeugt eine lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten.
Was ist eine nichtlineare Differentialgleichung?
Gleichungen, die nichtlineare Begriffe enthalten, werden als nichtlineare Differentialgleichungen bezeichnet.
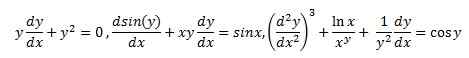
Alle oben genannten sind nichtlineare Differentialgleichungen. Nichtlineare Differentialgleichungen sind schwer zu lösen. Daher ist eine enge Studie erforderlich, um eine korrekte Lösung zu erhalten. Im Falle partieller Differentialgleichungen haben die meisten Gleichungen keine allgemeine Lösung. Daher muss jede Gleichung unabhängig behandelt werden.
Navier-Stokes-Gleichung und Euler-Gleichung in der Fluiddynamik, Einsteins Feldgleichungen der allgemeinen Relativitätstheorie sind bekannte nichtlineare partielle Differentialgleichungen. Manchmal kann die Anwendung der LaGrange -Gleichung auf ein variables System zu einem System nichtlinearer partieller Differentialgleichungen führen.
Was ist der Unterschied zwischen linearen und nichtlinearen Differentialgleichungen?
• Eine Differentialgleichung, die nur die linearen Begriffe der unbekannten oder abhängigen Variablen und seiner Derivate aufweist, wird als lineare Differentialgleichung bezeichnet. Es hat keinen Term mit der abhängigen Variablen des Index über 1 und enthält kein Vielfaches seiner Derivate. Es können keine nichtlinearen Funktionen wie trigonometrische Funktionen, exponentielle Funktionen und logarithmische Funktionen in Bezug auf die abhängige Variable haben. Jede Differentialgleichung, die oben genannte Begriffe enthält, ist eine nichtlineare Differentialgleichung.
• Lösungen linearer Differentialgleichungen erstellen Vektorraum und der Differentialoperator ist auch ein linearer Operator im Vektorraum.
• Lösungen linearer Differentialgleichungen sind relativ einfacher, und allgemeine Lösungen existieren. Für nichtlineare Gleichungen existiert in den meisten Fällen die allgemeine Lösung nicht und die Lösung kann problemspezifisch sein. Dies macht die Lösung viel schwieriger als die linearen Gleichungen.


