Unterschied zwischen Matrix und Determinante

Matrix gegen Determinante
Matrizen und Determinanten sind wichtige Konzepte sind lineare Algebra, bei denen Matrizen eine kurze Möglichkeit bieten, große lineare Gleichungen und Kombinationen darzustellen, während Determinanten einzigartig mit einer bestimmten Art von Matrizen zusammenhängen.
Mehr über Matrix
Matrizen sind rechteckige Arrays von Zahlen, bei denen die Zahlen in Zeilen und Spalten angeordnet sind. Die Anzahl der Spalten und Zeilen in einer Matrix bestimmen die Größe der Matrix. Im Allgemeinen wird eine Matrix identisch durch quadratische Klammern dargestellt, und die Zahlen sind in Reihen und Spalten im Inneren ausgerichtet.

A ist als 3 × 3 -Matrix bekannt, weil es 3 Spalten und 3 Zeilen enthält. Die von A_IJ gekennzeichneten Zahlen werden als Elemente bezeichnet und durch die Zeilennummer und die Spaltennummer eindeutig identifiziert. Außerdem kann die Matrix als [a_ij] _ (3 × 3) dargestellt werden, aber ihre Verwendung sind begrenzt, da die Elemente nicht explizit angegeben sind. Erweiterung des obigen Beispiels auf einen allgemeinen Fall können wir eine allgemeine Matrix der Größe M × n definieren;
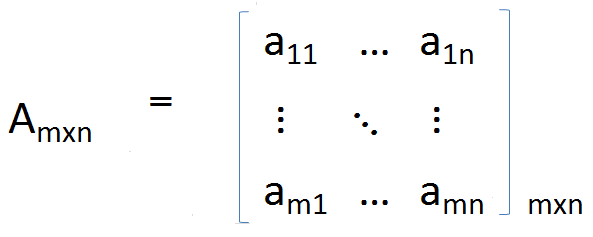
A hat M -Zeilen und N -Spalten.
Matrizen werden anhand ihrer besonderen Eigenschaften kategorisiert. Beispiel.
Operationen zu Matrizen werden speziell definiert, befolgen jedoch die Regeln in abstrakter Algebra. Daher werden Addition, Subtraktion und Multiplikation zwischen Matrizen an einem Element angezeigt. Bei Matrizen ist die Teilung nicht definiert, obwohl der Umkehrung existiert.
Matrizen sind eine kurze Darstellung einer Sammlung von Zahlen und können leicht zur Lösung linearer Gleichung verwendet werden. Matrizen haben auch eine breite Anwendung im Bereich der linearen Algebra, was lineare Transformationen betrifft.
Mehr über Determinante
Die Determinante ist eine eindeutige Zahl, die jeder Quadratmatrix zugeordnet ist und nach einer bestimmten Berechnung für die Elemente in der Matrix erhalten wird. In der Praxis wird eine Determinante dadurch bezeichnet, ein Modulzeichen für die Elemente in die Matrix zu setzen. Daher wird die Determinante von a gegeben;
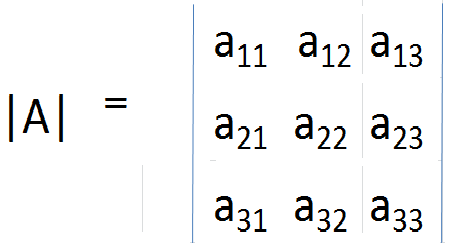
und im Allgemeinen für eine m × n Matrix
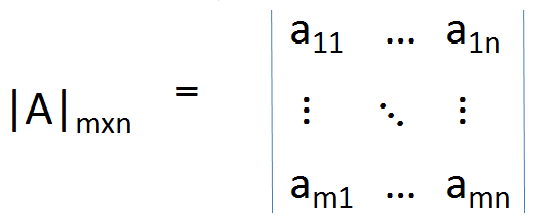
Die Operation zum Erhalt der Determinante ist wie folgt;
| A | = ∑NJ = 1 AJ Cij, wo Cij ist der Cofaktor der von c gegebenen Matrixij = (-1)i+j Mij.
Die Determinante ist ein wichtiger Faktor, der die Eigenschaften der Matrix bestimmt. Wenn die Determinante für eine bestimmte Matrix Null ist, existiert die Umkehrung der Matrix nicht.
Was ist der Unterschied zwischen Matrix und Determinant?
• Eine Matrix ist eine Gruppe von Zahlen, und eine Determinante ist eine eindeutige Zahl, die sich auf diese Matrix bezieht.
• Eine Determinante kann aus quadratischen Matrizen erhalten werden, aber nicht umgekehrt. Eine Determinante kann keine eindeutige Matrix geben.
• Die Algebra über die Matrizen und Determinanten hat Ähnlichkeiten und Unterschiede. Besonders bei Multiplikationen. Beispielsweise muss die Multiplikation von Matrizen ein Element erfolgen, wenn Determinanten einzelne Zahlen sind und die einfache Multiplikation folgen.
• Determinanten werden verwendet, um die Umkehrung der Matrix zu berechnen, und wenn die Determinante Null ist, existiert die Umkehrung der Matrix nicht.