Unterschied zwischen Parallelogramm und Trapez

Parallelogramm gegen Trapez
 

Parallelogramm und Trapez (oder Trapez) sind zwei konvexe Vierecke. Obwohl dies Vierecke sind, unterscheidet sich die Geometrie des Trapezs signifikant von den Parallelogrammen.

Parallelogramm

Parallelogramm kann als die geometrische Figur mit vier Seiten definiert werden, wobei die gegenüberliegenden Seiten parallel zueinander sind. Genauer gesagt ist es ein Viereck mit zwei Paaren paralleler Seiten. Diese parallele Natur verleiht den Parallelogrammen viele geometrische Eigenschaften.

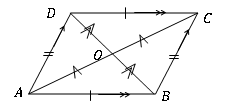
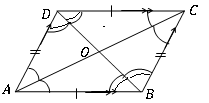
Ein Viereck ist ein Parallelogramm, wenn folgende geometrische Eigenschaften gefunden werden.

• Zwei Paare von gegnerischen Seiten sind gleich lang. (AB = DC, AD = BC)

• Zwei Paare von Gegnerwinkeln sind gleich groß. ([Latex] d \ Hat a b = b \ Hat c d, a \ Hat d c = a \ Hat b c [/latex])

• Wenn die benachbarten Winkel ergänzend sind [Latex] d \ Hat a b + a \ Hat d c = a \ Hat d c + b \ Hat c d = b \ Hat C D + A \ Hat b c = a \ Hat b c + d \ Hat a b = 180^\ circ = \ pi rad [/latex]

• Ein Paar Seiten, die sich gegenseitig gegenseitig widersprechen, ist parallel und gleich lang. (AB = DC & AB∥DC)

• Die Diagonalen halbieren sich gegenseitig (ao = oc, bo = od)

• Jede diagonale teilt das Viereck in zwei kongruente Dreiecke. (∆ADB ≡ ∆BCD, ∆ABC ≡ ∆ADC)

Ferner ist die Summe der Quadrate der Seiten gleich der Summe der Quadrate der Diagonalen. Dies wird manchmal als die bezeichnet Parallelogrammgesetz und hat weit verbreitete Anwendungen in Physik und Technik. (Ab² + BC² + CD² + Da² = AC² + Bd²)

Jedes der oben genannten Eigenschaften kann als Eigenschaften verwendet werden, sobald festgestellt wurde, dass das Viereck ein Parallelogramm ist.

Die Fläche des Parallelogramms kann durch das Produkt der Länge einer Seite und der Höhe auf die gegenüberliegende Seite berechnet werden. Daher kann der Bereich des Parallelogramms als angegeben werden

Fläche von Parallelogramm = Basis × Höhe = Ab×H

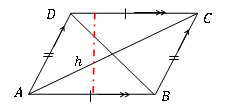
Der Bereich des Parallelogramms ist unabhängig von der Form des individuellen Parallelogramms. Es hängt nur von der Basislänge und der senkrechten Höhe ab.

Wenn die Seiten eines Parallelogramms durch zwei Vektoren dargestellt werden können, kann die Fläche durch die Größe des Vektorprodukts (Kreuzprodukt) der beiden benachbarten Vektoren erhalten werden.

Wenn die Seiten AB und AD durch die Vektoren ([Latex] \ Overrightarrow ab [/latex]) und ([laTex] \ Overrightarrow ad [/latex]) dargestellt werden, ist der Bereich des Parallelogramms durch [[ latex] \ links | \ Overrightarrow ab \ Times \ OverRightarrow ad \ right | = Ab \ cdot ad \ sin \ alpha [/latex], wobei α der Winkel zwischen [Latex] \ Overrightarrow ab [/latex] und [latex] \ Overrightarrow ad [/latex] ist, ist der Winkel. 

Im Folgenden finden Sie einige fortgeschrittene Eigenschaften des Parallelogramms;

• Der Bereich eines Parallelogramms ist doppelt so hoch wie ein Dreieck, das von einer seiner Diagonalen erzeugt wird.

• Der Bereich des Parallelogramms wird durch jede Linie, die durch den Mittelpunkt verläuft, in zwei Hälften aufgeteilt.

• Jede nicht enterne affine Transformation führt ein Parallelogramm in ein anderes Parallelogramm

• Ein Parallelogramm hat eine Rotationssymmetrie der Ordnung 2

• Die Summe der Entfernungen von einem Innenraum eines Parallelogramms zu den Seiten ist unabhängig vom Ort des Punktes

Trapez

Trapez (oder Trapez im britischen Englisch) ist ein konvexer Viereck, bei dem mindestens zwei Seiten parallel und ungleich sind. Die parallelen Seiten des Trapezes werden als Basen bezeichnet und die anderen beiden Seiten werden die Beine genannt.

Im Folgenden finden Sie Hauptmerkmale von Trapezoiden;

• Wenn sich die angrenzenden Winkel nicht auf derselben Basis des Trapezs befinden, sind sie ergänzende Winkel. ich.e. Sie addieren bis zu 180 ° ([Latex] b \ Hat a d+a \ Hat d c = a \ Hat b c+b \ Hat c d = 180^\ circ [/ Latex])

• Beide Diagonalen eines Trapeziums kreuzen sich im gleichen Verhältnis (das Verhältnis zwischen dem Abschnitt der Diagonalen ist gleich).

• Wenn A und B Basen sind und C, D Beine sind, sind die Längen der Diagonalen gegeben  

[latex] \ sqrt \ frac ab^2 -a^2 b-Ac^2+bd^2 b-a [/latex] 

Und

[latex] \ sqrt \ frac ab^2 -a^2 b-Ac^2+bc^2 b-a [/latex]

Die Fläche des Trapezs kann unter Verwendung der folgenden Formel berechnet werden

Bereich der Trapez = [Latex] \ Frac A+B 2 \ Times H [/latex]

Was ist der Unterschied zwischen Parallelogramm und Trapez (Trapez)?

• Sowohl Parallelogramm als auch Trapez sind konvexe Vierecke.

• In einem Parallelogramm sind beide Paare der gegnerischen Seiten parallel, während in einem Trapez nur ein Paar parallel ist.

• Die Diagonalen des Parallelogramms halben sich gegenseitig (1: 1 -Verhältnis), während sich die Diagonalen des Trapezes mit einem konstanten Verhältnis zwischen den Abschnitten kreuzen.

• Die Fläche des Parallelogramms hängt von der Höhe und der Basis ab, während die Fläche des Trapezs von der Höhe und dem mittleren Segment abhängt.

• Die beiden Dreiecke, die durch eine Diagonale in einem Parallelogramm gebildet werden.