Unterschied zwischen Beziehung und Funktion

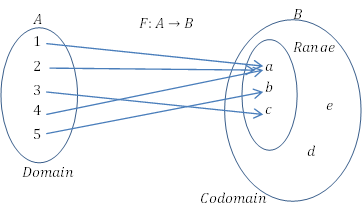
Beziehung vs Funktion
 

Ab der Mathematik der High School wird die Funktion zu einem gemeinsamen Begriff. Auch wenn es ziemlich oft verwendet wird, wird es ohne ordnungsgemäßes Verständnis seiner Definition und Interpretationen verwendet. Dieser Artikel konzentriert sich auf die Beschreibung dieser Aspekte einer Funktion.

Beziehung

Eine Beziehung ist ein Zusammenhang zwischen den Elementen zweier Sätze. In einer formaleren Umgebung kann es als Teilmenge des kartesischen Produkts von zwei Sätzen x und y beschrieben werden. Das kartesische Produkt von X und Y, bezeichnet als X × Y, ist eine Reihe von geordneten Paaren, die aus Elementen aus den beiden Sätzen bestehen, die oft als (als (x, y). Die Sets müssen nicht anders sein. Zum Beispiel wird eine Untergruppe von Elementen aus einem × A als Beziehung zu a bezeichnet.

Funktion

Funktionen sind eine besondere Art von Beziehungen. Diese spezielle Art von Beziehung beschreibt, wie ein Element einem anderen Element in einem anderen Satz oder demselben Satz zugeordnet ist. Damit die Beziehung eine Funktion ist, müssen zwei spezifische Anforderungen erfüllt sein.

Jedes Element des Satzes, an dem jede Zuordnung beginnt.

Die Elemente im Set, bei dem Mapping beginnt

Der Satz, aus dem die Beziehung zugeordnet ist. Das Set, in das die Beziehung zugeordnet ist, ist als Codomäne bekannt. Die Teilmenge der Elemente in der Codomäne, die nur die mit der Beziehung verbundenen Elemente enthalten.

Technisch gesehen ist eine Funktion eine Beziehung zwischen zwei Sätzen, wobei jedes Element in einem Satz ein Element in der anderen einzigartig zugeordnet ist.

 Beachten Sie Folgendes

• Jedes Element in der Domäne wird in die Codomäne abgebildet.
• Mehrere Elemente der Domäne sind im Codomäne mit demselben Wert verbunden, aber ein einzelnes Element aus der Domäne kann nicht mit mehr als einem Element der Codomäne verbunden werden. (Mapping muss einzigartig sein)
• Wenn jedes einzelne Element der Domäne in unterschiedliche und einzigartige Elemente in der Codomäne abgebildet wird, soll die Funktion eine „Eins-zu-Eins“ -Funktion sein.

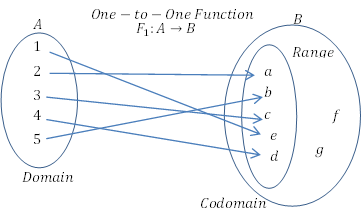
• Die Codomäne enthält andere als diejenigen, die mit den Elementen der Domäne verbunden sind. Der Bereich muss nicht die Codomäne sein. Wenn die Codomäne gleich dem Bereich ist, wird die Funktion als "auf" -Funktion bezeichnet.

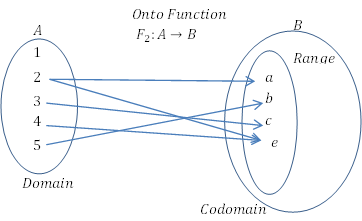
Wenn die Werte, die von der Funktion genommen werden können, real sind, wird sie als echte Funktion bezeichnet. Die Elemente von Codomäne und Domäne sind reelle Zahlen.

Funktionen werden immer mit Variablen bezeichnet. Die Elemente der Codomäne werden symbolisch durch die Variable dargestellt. Die Notation f (x) repräsentiert die Elemente des Bereichs. Die Beziehung kann unter Verwendung des Ausdrucks in Form f (x) = x^2 dargestellt werden. Es heißt, dass das Element der Domäne im Quadrat des Elements innerhalb der Codomäne abgebildet ist. 

Was ist der Unterschied zwischen Funktion und Beziehung?

• Funktionen sind eine besondere Art von Beziehungen.

• Die Beziehung basiert auf dem kartesischen Produkt von zwei Sätzen.

• Die Funktion basiert auf Beziehungen mit bestimmten Eigenschaften.

• Die Domäne einer Funktion muss so in die Codomäne abgebildet werden. Die Beziehung kann ein einzelnes Element mit mehreren Werten verknüpfen.