Unterschied zwischen sin 2x und 2 sin x

Sünde 2x gegen 2 Sünde x
Funktionen sind eine der wichtigsten Klassen mathematischer Objekte. Die Sinusfunktion, die als bezeichnet wird als F(X) = sin X ist eine trigonometrische Funktion, die aus dem Satz realer Zahlen auf das Intervall [-1, 1] definiert ist und mit Periode 2 ᴫ regelmäßig ist.
Die grundlegende Definition des Sinus eines akuten Winkels erfolgt unter Verwendung eines rechtwinkligen Dreiecks. Der Sinus des Winkels ist gleich dem Verhältnis der Länge der Seite gegenüber einem Winkel zur Länge der Hypotenuse. Diese Definition kann auf alle Winkel mit der Identitätssünde erweitert werden (-X) = - sin X und Sünde (ᴫ + X) = - sin X und Sünde (2Nᴫ + X) = sin X.
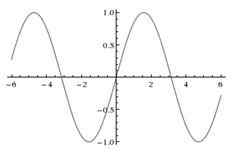
Für die nächsten beiden Abschnitte berücksichtigen F(X) = sin X Und G(X) = 2X.
Was ist Sünde 2x?
Betrachten Sie die zusammengesetzte Funktion Nebel gegeben durch Nebel (X) = F (G(X)) = F(2X) = sin 2X. Diese Funktion ist der Sünde ziemlich ähnlich X mit der Domäne als Satz von reellen Zahlen und dem Bereich als Intervall [-1, 1]. Diese Funktion ist periodisch mit der Periode ᴫ (im Gegensatz zu der Zeit 2ᴫ der Sünde X). Sünde 2X kann durch die Identitätssünde 2 erweitert werdenX = 2 Sünde X cos X zu.
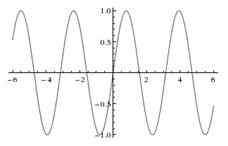
Was ist 2 Sin x?
Betrachten Sie die zusammengesetzte Funktion g o f gegeben durch g o f (X) = G (F(X)) = G (Sünde X) = 2 sin X. Dies ist auch eine periodische Funktion mit der gleichen Zeit wie die Sünde X, aber doppelt so hoch wie die Amplitude seit -1 ≤ sin X ≤ 1 impliziert -2 ≤ 2 sin X ≤ 2. Seine Domäne ist der Satz realer Zahlen und der Bereich ist das Intervall [-2, 2]
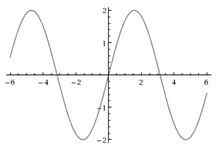
| Was ist der Unterschied zwischen Sin 2x und 2 sin x? • SIN 2x wird aus dem Satz realer Zahlen auf das Intervall [-1, 1] definiert, während 2Sin x aus dem Satz realer Zahlen auf das Intervall [-2, 2] definiert wird. • sin 2x ist periodisch mit Periode ᴫ, aber 2 sin x ist periodisch mit Periode 2ᴫ. |


