Was ist der Unterschied zwischen Fraunhofer und Fresnel -Beugung

Der Schlüsselunterschied zwischen Fraunhofer und Fresnel -Beugung ist, dass die Fraunhofer -Beugungsgleichung die Modellierung der Beugung von Wellen mit einem Beugungsmuster mit einem langen Abstand vom Beugungsobjekt beinhaltet.
Die Beugung ist ein Phänomen, das als Lichtstreuung um ein Objekt bezeichnet werden kann, wenn ein Lichtstrahl teilweise durch das Objekt blockiert wird, wo wir dunkle und helle Bänder am Rand des Schattens dieses Objekts sehen können.
INHALT
1. Überblick und wichtiger Unterschied
2. Was ist Fraunhofer -Beugung
3. Was ist Fresnel -Beugung
4. Fraunhofer gegen Fresnel -Beugung in tabellarischer Form
5. Zusammenfassung
Was ist Fraunhofer -Beugung?
Fraunhofer -Beugung ist eine Gleichung, die bei der Modellierung der Beugung von Wellen nützlich ist. Darüber hinaus können wir diese Gleichung zur Modellierung der Beugung von Wellen verwenden, wenn das Beugungsmuster in der Fokusebene einer Bildweite erscheint. Diese Gleichung wurde nach dem Wissenschaftler Joseph von Fraunhofer benannt.
Wir können die Auswirkungen der Beugung unter Verwendung des Huygens-Fresnel-Prinzips modellieren, wobei Huygens postulierten, dass die Punkte an einer primären Wellenfront als Quelle sphärischer sekundärer Wavelets wirken können, und wir können die Summe dieser sekundären Wavelets verwenden, um die Form der Form des Welle, die zu jeder späteren Zeit fortschreitet. Diese Zugabe von Wavelets umfasst viele Wellen unterschiedlicher Phasen und Amplituden. E.G. Die Zugabe von zwei Wellen mit gleicher Amplitude (die in Phase) kann zu einer Verschiebung mit einer doppelten Amplitude führen.
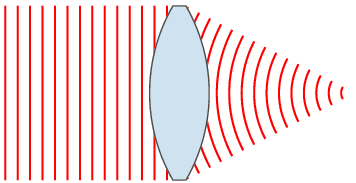
Wenn wir die Beugung bestimmen, die auftritt, wenn es einen Abstand zwischen der Apertur und der Beobachtungsebene besteht. Daher kann der Ausbreitungsweg für einen Wavelet als parallel von jedem Punkt der Apertur bis zum Beobachtungspunkt angesehen werden. Dieses Phänomen wird als Fernfeld bezeichnet, und wir können die Fraunhofer-Beugungsgleichung verwenden, um diese Art von Beugung zu modellieren.
Was ist Fresnel -Beugung?
Die Fresnel -Beugung ist eine Gleichung, die wir auf die Ausbreitung von Wellen im Nahen Feld anwenden können. Daher wird es auch in der Nähe des Feldbeugung bezeichnet. Es ist eine Annäherung an die Kirchhoff-Fresnel-Beugung. Wir können diese Gleichung verwenden, um das Beugungsmuster zu berechnen, das durch die Wellen erzeugt wird, die durch eine Blende oder um ein Objekt gehen.

Diese Gleichung führt die Fresnel -Nummer F der optischen Anordnung ein. Wenn diese Zahl höher als 1 ist, können wir berücksichtigen, dass sich die gebeugte Welle im Nahfeld befindet. Die Gültigkeit dieser Näherung hängt jedoch vom Winkel der Welle ab. Die Fresnel -Beugungsgleichung wurde von Francesco Maria Grimaldi (Italien) in der 17 eingeführtth Jahrhundert. Er verwendete das Prinzip von Huygens, um zu untersuchen, was sich während der Beugung abspielt.
Was ist der Unterschied zwischen Fraunhofer und Fresnel -Beugung?
Fraunhofer -Beugung ist eine Gleichung, die bei der Modellierung der Beugung von Wellen nützlich ist. Die Fresnel -Beugung ist eine Gleichung, die wir auf die Ausbreitung von Wellen im Nahen Feld anwenden können. Der Schlüsselunterschied zwischen Fraunhofer und Fresnel -Beugung besteht darin, dass die Fraunhofer -Beugung -Gleichung die Modellierung der Beugung von Wellen mit einem Beugungsmuster mit einem langen Abstand vom Beugung Objekt auftritt Objekt.
Die folgende Tabelle fasst den Unterschied zwischen Fraunhofer und Fresnel -Beugung zusammen.
Zusammenfassung -Fraunhofer gegen Fresnel -Beugung
Der Schlüsselunterschied zwischen Fraunhofer und Fresnel -Beugung besteht darin, dass die Fraunhofer -Beugung -Gleichung die Modellierung der Beugung von Wellen mit dem Beugungsmuster bei einem langen Abstand vom Beugungsobjekt auftritt Objekt.
Referenz:
1. „Fresnel -Beugung.” Wikipedia, Wikimedia Foundation, 19. Mai 2021.
Bild mit freundlicher Genehmigung:
1. "Objektiv und Wellenfronts gedreht" von EPZCAW - eigener Arbeit (CC BY -SA 3.0) über Commons Wikimedia
2. "Kreisende Apertur Fresnel -Beugung High Res" von Gisling - eigene Arbeit (CC BY -SA 3.0) über Commons Wikimedia


