Differenz zwischen Fixpunkt und Gleichgewichtspunkt
Der Schlüsselunterschied Zwischen Fixpunkt und Gleichgewichtspunkt befindet sich das Der feste Punkt ist nützlich, um den stationären Zustand eines Systems zu finden, während der Gleichgewichtspunkt der Zustand ist, in dem sich das System nicht ändert, wenn sich die Systemvariablen ändernD.
Fixpunkt- und Gleichgewichtspunkt sind nützliche Begriffe in der Mathematik, um den stationären Zustand eines gewünschten physikalischen Systems zu identifizieren.
INHALT
1. Überblick und wichtiger Unterschied
2. Was ist Fixpunkt
3. Was ist Gleichgewichtspunkt?
4. Ähnlichkeiten zwischen Fixpunkt und Gleichgewichtspunkt
5. Seite für Seitenvergleich - Fixpunkt gegen Gleichgewichtspunkt in tabellarischer Form
6. Zusammenfassung
Was ist Fixpunkt?
Der feste Punkt einer Funktion in der Mathematik ist ein Element der Domäne dieser Funktion, die durch die Funktion auf sich selbst zugeordnet werden kann. Mit anderen Worten, "C" ist ein fester Punkt der Funktion "f", wenn f (c) = c. Dies ist auch als Fixpoint oder invarianter Punkt bekannt. Daher ist f (f (… f (c)…)) = fN(c) = C, was ein wichtiges Beendigung der Beendigung der rekursiven Berechnung von „F“ ist. Wir können einen Satz von Fixpunkten als fester Satz benennen.
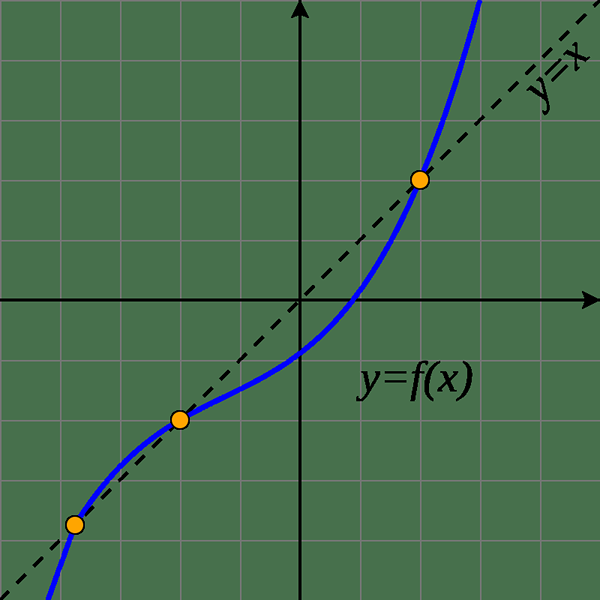
Betrachten wir ein Beispiel, um dieses Phänomen zu verstehen. Wenn wir "f" in realer Zahlen durch f (x) = x nehmen2 - 3x +4, dann ist 2 ein fester Punkt von „f“, weil f (2) = 2. Alle Funktionen haben jedoch keine festen Punkte. E.G. Wenn f (x) = x + 1, gibt es keine Fixpunkte, da „x“ für eine reelle Zahl niemals „x +1“ entspricht. In Anbetracht der grafischen Terminologie bezieht sich ein fester Punkt „x“ auf den Punkt (x, f (x)), der sich in der Linie y = x befindet. Mit anderen Worten, die Grafik von „F“ enthält einen gemeinsamen Punkt mit dieser Zeile.

Fixpunkte sind periodische Punkte, die ihre Periode entsprechen einer einer. In Anbetracht der projektiven Geometrie werden die Fixpunkte einer Projektivität als doppelte Punkte bezeichnet. Nach der Galois -Theorie wird die Reihe von Fixpunkten einer Reihe von Feldautomorphismen als festes Feld dieser Automorphismen bezeichnet.
Es gibt unterschiedliche Anwendungen von Fixpunkten, einschließlich Ökonomie, Physik, Programmiersprache Compiler, Typtheorie, Vektor auf PageRank -Werten aller Webseiten, der stationären Verteilung der Markov -Kette usw.
Was ist Gleichgewichtspunkt??
Ein Gleichgewichtspunkt ist eine konstante Lösung für eine andere Gleichung in der Mathematik. Dieser Begriff kommt hauptsächlich unter Differentialgleichungen in der Mathematik. Wir können die Gleichgewichte klassifizieren, indem wir die Zeichen der Eigenwerte der Linearisierung der Gleichungen über die Gleichgewichte beobachten. Mit anderen Worten, wir können Gleichgewichte kategorisieren, indem wir die jakobische Matrix an den Gleichgewichtspunkten des gewünschten Systems bewerten, gefolgt von der Suche nach den resultierenden Eigenwerten. Dort können wir das Verhalten des Systems in der Nachbarschaft der Gleichgewichtspunkte quantitativ bestimmen, indem wir den Eigenvektor (en) ermitteln, der mit den Eigenwerten verbunden ist.
Wir können sagen, dass ein Gleichgewichtspunkt hyperbolisch ist, wenn keiner der Eigenwerte keinen realen Teil hat. Wenn jedoch alle Eigenwerte einen negativen realen Teil haben, wird das Gleichgewicht zu einer stabilen Gleichung. In ähnlicher Weise wird das Gleichgewicht, wenn es einen positiven realen Teil gibt, instabil. Wenn es mindestens einen negativen realen Teil und mindestens einen positiven realen Teil in Eigenwerten gibt, erhält das Gleichgewicht einen Sattelpunkt.
Was sind die Ähnlichkeiten zwischen Fixpunkt und Gleichgewichtspunkt??
- Diese Punkte sind möglicherweise nicht stabil.
- Beide Punkte werden für einen stationären Zustand eines Systems beschrieben.
Was ist der Unterschied zwischen Fixpunkt und Gleichgewichtspunkt??
Die Begriffe Fixpunkt- und Gleichgewichtspunkt werden in der Mathematik verwendet. Der Schlüsselunterschied zwischen Fixpunkt und Gleichgewichtspunkt besteht darin, dass Fixpunkt nützlich ist, um den stationären Zustand eines Systems zu finden.

Zusammenfassung -Fixpunkt gegen Gleichgewichtspunkt
Fixpunkt- und Gleichgewichtspunkt sind nützliche Begriffe in der Mathematik, um den stationären Zustand eines gewünschten physikalischen Systems zu identifizieren. Der Schlüsselunterschied zwischen Fixpunkt und Gleichgewichtspunkt besteht darin, dass Fixpunkt nützlich ist, um den stationären Zustand eines Systems zu finden.
Referenz:
1. „Fixpunkt (Mathematik).” Wikipedia, Wikimedia Foundation, 26. März. 2021, hier erhältlich.
Bild mit freundlicher Genehmigung:
1. „Beispiel für feste Punkte“ von Krishnavedala - eigene Arbeit (CC0) über Commons Wikimedia