Unterschied zwischen Hyperbola und Ellipse
Hyperbola gegen Ellipse
Wenn ein Kegel in verschiedenen Winkeln geschnitten wird, werden verschiedene Kurven durch die Kante des Kegels gekennzeichnet. Diese Kurven werden oft als konische Abschnitte bezeichnet. Genauer gesagt ist ein Kegelabschnitt eine Kurve. In verschiedenen Schnittwinkeln werden verschiedene konische Abschnitte angegeben.
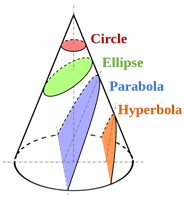
Sowohl Hyperbola als auch Ellipse sind konische Abschnitte, und ihre Unterschiede können in diesem Zusammenhang leicht verglichen werden.
Mehr über Ellipse
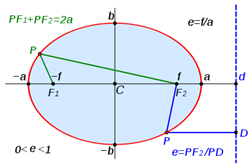
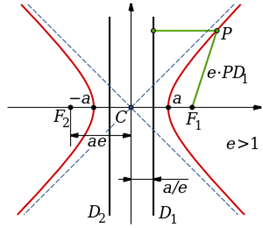
Wenn der Schnittpunkt der Kegeloberfläche und der Ebeneoberfläche eine geschlossene Kurve erzeugt, ist sie als Ellipse bekannt. Es hat eine Exzentrizität zwischen Null und einem (0 Das Liniensegment, das durch die Herde verläuft. Die Durchmesser entlang jeder Achse sind als Querdurchmesser bzw. der Konjugatdurchmesser bekannt. Die Hälfte der Hauptachse ist als Semi-Major-Achse bekannt, und die Hälfte der Nebenachse ist als Semi-Minor-Achse bekannt. Jeder Punkt f1 und f2 sind als die Zeugen der Ellipse und der Längen bekannt F1 + Pf2 = 2a , Wo P ist ein willkürlicher Punkt auf der Ellipse. Exzentrizität e ist definiert als das Verhältnis zwischen dem Abstand von einem Fokus zum willkürlichen Punkt ( Pf2 ) und der senkrechte Abstand zum willkürlichen Punkt vom Directrix (PD). Es entspricht auch dem Abstand zwischen den beiden Foki und der Semi-Major-Achse: e = PF/PD = Fa Die allgemeine Gleichung der Ellipse, wenn die halbmagierende Achse und die Semi-Minor-Achse mit den kartesischen Achsen zusammenfallen, wird wie folgt angegeben. X2/A2 + y2/B2 = 1 Die Geometrie der Ellipse hat viele Anwendungen, insbesondere in der Physik. Die Umlaufbahnen der Planeten im Sonnensystem sind elliptisch mit der Sonne als einen Fokus. Die Reflektoren für Antennen und akustische Geräte werden in elliptischer Form hergestellt, um die Tatsache zu nutzen. Mehr über Hyperbel Die Hyperbel ist ebenfalls ein Kegelabschnitt. Der Begriff Hyperbola wird auf die beiden in der Abbildung gezeigten getrennten Kurven verwiesen. Anstatt wie eine Ellipse die Arme oder die Zweige der Hyperbel bis in die Unendlichkeit zu schließen. Die Punkte, an denen die beiden Zweige den kürzesten Abstand zwischen ihnen haben. Die durch die Scheitelpunkte verlaufende Linie wird als Hauptachse oder Querachse angesehen und ist eine der Hauptachsen der Hyperbel. Die beiden Schwerpunkte der Parabel liegen ebenfalls auf der Hauptachse. Der Mittelpunkt der Linie zwischen den beiden Scheitelpunkten ist die Mitte, und die Länge des Liniensegments ist die Halb-Major-Achse. Der senkrechte Halbierektor der Semi-Major-Achse ist die andere Hauptachse, und die beiden Kurven der Hyperbel sind symmetrisch um diese Achse. Die Exzentrizität der Parabel ist größer als eins; e> 1. Wenn die Hauptachsen mit den kartesischen Achsen übereinstimmen, ist die allgemeine Gleichung der Hyperbel von der Form: X2/A2 - y2/B2 = 1, Wo A ist die Semi-Major-Achse und B ist die Entfernung vom Zentrum zu beiden Fokus. Die Hyperbel mit offenen Enden, die der X-Achse ausgerichtet sind. Ähnliche Hyperbel können auch auf der Y -Achse erhalten werden. Diese sind als Y-Achse-Hyperbolas bekannt. Die Gleichung für solche Hyperbolas nimmt die Form an y2/A2 - X2/B2 = 1 Was ist der Unterschied zwischen Hyperbola und Ellipse? • Sowohl Ellipsen als auch Hyperbola sind konische Abschnitte, aber die Ellipse ist eine geschlossene Kurve, während die Hyperbel aus zwei offenen Kurven besteht. • Daher hat die Ellipse ein begrenztes Umfang, aber die Hyperbel hat eine unendliche Länge. • Beide sind symmetrisch um ihre Haupt- und Nebenachse, aber die Position des Directrix ist jeweils unterschiedlich. In der Ellipse liegt sie außerhalb der halbmagierenden Achse, während es in Hyperbola in der halbmagierenden Achse liegt. • Die Exzentrizitäten der beiden Kegelabschnitte sind unterschiedlich. 0 eHyperbel > 0 • Die allgemeine Gleichung der beiden Kurven sieht gleich aus, aber sie sind unterschiedlich. • Senkrechter Halbierektor der Major-Achse schneidet die Kurve in der Ellipse, jedoch nicht in der Hyperbel. (Bilderquelle: Wikipedia)