Unterschied zwischen lokalem und globalem Maximum

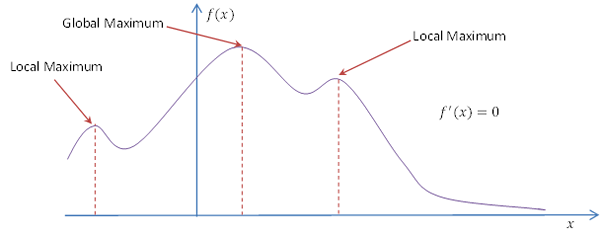
Lokal gegen Global Maximum
 

Der größte Wert eines Satzes oder einer Funktion wird als maximal bezeichnet. Betrachten Sie den Satz a_ich | i ∈ N. Das Element a_k wo ein_k ≥ a_ich Für alles ist ich als maximales Element des Satzes bekannt. Wenn das Set bestellt wird, wird es das letzte Element des Satzes.

Nehmen Sie zum Beispiel den Satz a = 1,6,9,2,4,8,3. In Anbetracht aller Elemente ist 9 größer als jedes andere Element im Satz. Daher ist es das maximale Element des Satzes. Durch Bestellung des Sets erhalten wir a = 1,2,3,4,6,8,9. Im bestellten Satz ist 9 (das maximale Element) das letzte Element.

Lokales Maximum

Der größte Wert in einer Untergruppe oder einem Bereich einer Funktion ist als lokales Maximum bezeichnet. Es ist der größte Wert für die angegebene Untergruppe oder den Bereich, aber es kann andere Elemente geben, die größer sind als die außerhalb des bekannten Bereichs oder der Teilmenge. Es kann viele geben Lokale Maxima im Bereich der Funktion oder im Universal Set.

Betrachten Sie die Menge der Ganzzahlen 1 bis 10, s = 1,2,3,4,5,6,7,8,9,10. A ist eine Untergruppe der s. Maximal von a (9) ist nicht das Maximum für den gesamten Satz, das ist 10. Daher ist 9 ein lokales Maximum.

Globales Maximum

Der größte Gesamtwert einer Funktion oder ein Satz ist als globales Maximum bezeichnet. Ist eingestellt S, 10 ist das globale Maximum. Dieses Element ist größer als jeder Wert des Satzes. Wenn es eine Funktion ist, ist es größer als jeder andere Wert der Funktion über die gesamte Domäne des Satzes (größtes Element im Codomäne). Das globale Maximum einer Funktion oder ein Satz ist eindeutig (für diesen speziellen Fall). 

Im Falle einer Funktion ist der Maximalwert der Gradient der Funktion Null. Der Gradient kurz vor dem Maximum ist positiv und kurz danach negativ. Dies wird als Test verwendet, um lokale Maxima in Funktionen zu finden (erster Ableitungstest).

Was ist der Unterschied zwischen globalem Maximum und lokalem Maximum?

• Maximum ist das größte Element in einem Satz oder einem Bereich einer Funktion.

• Das globale Maximum ist der größte Wert unter den Gesamtelementen eines Satzes oder der Werte einer Funktion.

• Lokales Maximum ist das größte Element in einer Untergruppe oder einem bestimmten Bereich einer Funktion.

• Das globale Maximum ist einzigartig, während das lokale Maximum nicht ist. Es kann mehr als ein lokales Maximum geben. Wenn es nur ein lokales Maximum gibt, ist es das globale Maximum.