Unterschied zwischen Mittelwert, Median und Modus

Mittelwert gegen Median gegen Modus
 

Mittelwert, Median und Modus sind die primären Maße der zentralen Tendenz verwendet in beschreibenden Statistiken. Sie unterscheiden sich völlig voneinander und Fälle, in denen sie zur Zusammenfassung der Daten verwendet werden, sind ebenfalls unterschiedlich.

Bedeuten

Der arithmetische Mittelwert ist die Summe der Datenwerte geteilt durch die Anzahl der Datenwerte, i.e.

[Latex] \ bar x = \ frac 1 n \ sum_ i = 1^n x_ i = \ frac x_ 1+x_ 2+x_ 3 +… +X_ n n [/latex] 

Wenn die Daten aus einem Stichprobenraum stammen, wird sie als Beispielmittel ([Latex] \ bar x [/latex]) bezeichnet, was eine beschreibende Statistik der Stichprobe ist. Obwohl es das am häufigsten verwendete beschreibende Maß für eine Probe ist, ist es keine robuste Statistik. Es ist sehr empfindlich gegenüber den Ausreißern und Oszillationen.

Betrachten Sie beispielsweise das durchschnittliche Einkommen der Bürger einer bestimmten Stadt. Da alle Datenwerte summiert und dann geteilt werden, wirkt sich das Einkommen einer äußerst wohlhabenden Person erheblich auf den Mittelwert aus. Daher sind die Mittelwerte immer eine gute Darstellung der Daten immer.

Auch im Falle eines abwechselnden Signals variiert der Strom, der durch ein Element führt. Wenn wir den durchschnittlichen Strom in einem einzigen Zeitraum durch das Element nehmen, gibt er eine 0, was bedeutet, dass kein Strom das Element durchlaufen hat, was offensichtlich nicht wahr ist. Daher ist auch in diesem Fall das arithmetische Mittelwert kein gutes Maß.

Der arithmetische Mittelwert ist ein guter Indikator, wenn die Daten gleichmäßig verteilt sind. Für eine Normalverteilung entspricht der Mittelwert dem Modus und dem Median. Es hat auch die niedrigsten Residuen, wenn man den quadratischen Fehler des Stammwerts berücksichtigt. Daher ist die beste beschreibende Maßnahme, wenn es erforderlich ist, um einen Datensatz durch eine einzelne Zahl darzustellen.

Median

Die Werte des mittleren Datenpunkts nach dem Anordnen aller Datenwerte in aufsteigender Reihenfolge sind als Median des Datensatzes definiert. Median ist das 2. Quartil, das 5. Dezember und das 50. Perzentil.

• Wenn die Anzahl der Beobachtungen (Datenpunkte) ungerade ist, ist der Median genau die Beobachtung in der Mitte der geordneten Liste.

• Wenn die Anzahl der Beobachtungen (Datenpunkte) ausgeglichen ist, ist der Median der Mittelwert der beiden mittleren Beobachtungen in der geordneten Liste.

Der Median unterteilt die Beobachtung in zwei Gruppen; ich.e. eine Gruppe (50%) von Werten höher und eine Gruppe (50%) von Werten niedriger als der Median. Mediane werden speziell in verzerrten Verteilungen verwendet und stellen Daten ziemlich besser als der arithmetische Mittel dar.

Modus

Der Modus ist die auftretendste Zahl in einer Reihe von Beobachtungen. Der Modus eines Datensatzes wird berechnet, indem die Häufigkeit jedes Elements innerhalb des Satzes ermittelt wird.

• Wenn kein Wert mehr als einmal auftritt, hat der Datensatz keinen Modus.

• Andernfalls ist jeder Wert, der mit der größten Frequenz auftritt, ein Modus des Datensatzes.

Mehr als 1 Modus kann in einem Satz existieren; Der Modus ist daher keine eindeutige Statistik eines Datensatzes. In einer einheitlichen Verteilung gibt es einen Modus. Der Modus einer diskreten Wahrscheinlichkeitsverteilung ist der Punkt, an dem die Wahrscheinlichkeitsmassenfunktion ihren höchsten Punkt erreicht. Wenn wir uns aus den oben genannten Interpretationen abgeben, können wir das sagen Global Maxima sind Modi.

Betrachten Sie die Anwendung aller drei Maßnahmen auf den folgenden Datensatz.

Daten: 1, 1, 2, 3, 5, 5, 5, 5, 6, 6, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 14, 14, 15, 15 , 15

Mean = (1+ 1+ 2+ 3+ 5+ 5+ 5+ 5+ 6+ 6+ 8+ 8+ 9+ 9+ 9+ 9+ 10+ 10+ 10+ 14+ 14+ 15+ 15+ 15 ) / 25 = 8.12

Median = 9 (13. Element)

Modus = 9 (Frequenz von 9 = 5)

Was ist der Unterschied zwischen Mittelwert, Median und Modus?

• Arithmetischer Mittelwert ist die Summe der Werte (Beobachtungen) geteilt durch die Anzahl der Beobachtungen. Es ist keine robuste Statistik und hängt stark von der Normalverteilungsmerkmale innerhalb der betrachteten Verteilung ab. Ein einzelner Ausreißer kann eine signifikante Verschiebung des Mittelwerts verursachen, die relativ irreführende Werte ergeben. Das Konzept kann auf geometrischen Mittelwert, harmonischer Mittel, gewichteter Mittel und so weiter ausgedehnt werden.

• Der Median ist die mittleren Werte der Beobachtungsmenge und ist von Ausreißern relativ weniger beeinflusst. Es kann eine gute Einschätzung als zusammenfassende Statistik in stark verzerrten Fällen geben.

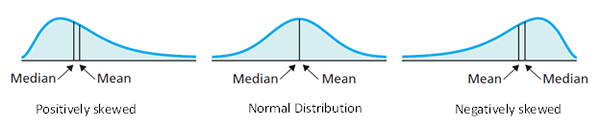
• Der Modus ist die häufigsten Beobachtungswerte im Datensatz. Wenn die Verteilung positiv verzerrt ist, liegt der Modus dem Median, und wenn negativ verzerrt ist, liegt der Modus direkt zum Median.

• Wenn sie positiv verzerrt sind, ist Mittelwert für den Median richtig; Wenn negativ verzerrt ist, liegt links vom Median.

• In der Normalverteilung sind alle drei, Mittelwert, Modus und Median gleich.