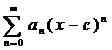Unterschied zwischen Power -Serien und Taylor -Serie

Power -Serie gegen Taylor -Serie
In der Mathematik ist eine echte Sequenz eine geordnete Liste realer Zahlen. Formal handelt es sich. Wenn ANist das nth Begriff einer Sequenz bezeichnen wir die Sequenz durch oder durch A1, A2,… ,AN,… .Betrachten Sie zum Beispiel die Sequenz 1, ½, ⅓,… , 1/N,… . Es kann als 1/n bezeichnet werden.
Es ist möglich, eine Reihe mit Sequenzen zu definieren. Eine Serie ist die Summe der Bedingungen einer Sequenz. Daher gibt es für jede Sequenz eine assoziierte Sequenz und umgekehrt. Wenn einN ist die untersuchte Sequenz, die durch diese Sequenz gebildete Reihe kann als:
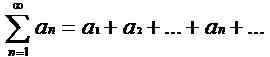
Somit ist im obigen Beispiel die zugehörige Serie 1+1/2+1/3+… + 1/N +… .
Wie die Namen vermuten lassen, ist die Power -Serie eine spezielle Art von Serien und wird in der numerischen Analyse und der verwandten mathematischen Modellierung ausführlich verwendet. Die Taylor-Serie ist eine spezielle Power-Serie, die eine alternative und leicht zu manipulierende Möglichkeit bietet, bekannte Funktionen darzustellen.
Was ist Power Series?
Eine Power -Serie ist eine Reihe der Form
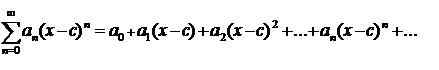
Welches ist (möglicherweise) in einem Intervall konvergent, der bei zentriert ist C. Die Koeffizienten AN Kann reale oder komplexe Zahlen sein und ist unabhängig von von X; ich.e. die Dummy -Variable.
Zum Beispiel durch Einstellen AN= 1 für jeden N, Und C = 0, die Power -Serie 1+x+x2+… + XN+… Wird erhalten. Es ist leicht zu beobachten, dass diese Leistungsreihe, wenn x ε (-1,1), zu 1/(1-x) konvergiert, dass diese Leistungsserie konvergiert, wenn er 1/(1-x) konvergiert.
Eine Power -Serie konvergiert, wenn X = C. Die anderen Werte von X für die die Power -Serie konvergiert wird immer in Form eines offenen Intervalls, der zentriert ist C. Das ist, Es wird einen Wert 0 ≤ geben R ≤ ∞ so dass für jeden X befriedigend | x-c | ≤R, Die Power -Serie ist konvergent und für jeden X befriedigend | x-c |>R, Die Power -Serie ist unterschiedlich. Dieser Wert R wird als Konvergenz der Power -Serie bezeichnet (R kann einen echten Wert oder einen positiven Unendlichkeit nehmen).
Power -Serien können mit den folgenden Regeln hinzugefügt, subtrahiert, multipliziert und geteilt werden. Betrachten Sie die beiden Power -Serien:
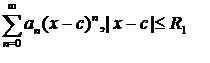
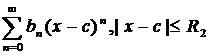 .
.
Dann,
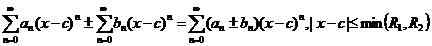
ich.e. gleiche Begriffe werden zusammengefügt oder zusammengezogen. Außerdem ist es möglich, die beiden Power -Serien mit der Identität zu multiplizieren und zu teilen,
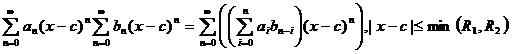
Was ist Taylor -Serie?
Die Taylor -Serie ist für eine Funktion definiert F(X) Das ist in einem Intervall unendlich differenzierbar. Annehmen F(X) ist in einem Intervall differenzierbar bei C. Dann die Power -Serie, die gegeben wird
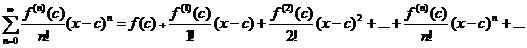
wird als Expansion der Funktion der Taylor -Serie bezeichnet F(X) um C. (Hier F(N)(C) Bezeichnen die nth Derivat bei X = C). In der numerischen Analyse wird eine begrenzte Anzahl von Begriffen in dieser unendlichen Expansion verwendet, um Werte an Punkten zu berechnen, an denen die Serie auf die ursprüngliche Funktion konvergent ist.
Eine Funktion F(X) soll im Intervall analytisch sein (a, b), wenn für jedes x ε (a, b) die Taylor -Serie von F(X) Konvergiert zur Funktion F(X). Zum Beispiel ist 1/(1-x) analytisch auf (-1,1), da seine Taylor-Expansion 1+x+x2+… + XN+… Konvergiert zur Funktion in diesem Intervall, und eX ist überall analyt, da die Taylor -Reihe von Taylor eXkonvergiert zu eX Für jede reelle Zahl X.
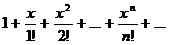
Was ist der Unterschied zwischen Power -Serien und Taylor -Serien?
1. Die Taylor -Serie ist eine spezielle Klasse von Power -Serien, die nur für Funktionen definiert sind, die in einigen offenen Intervall unendlich differenzierbar sind.
2. Taylor -Serie nimmt die besondere Form an
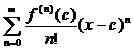
Während eine Power -Serie jede Reihe der Form sein kann