Unterschied zwischen Rechteck und Rhombus

Rechteck gegen Rhombus
Rhombus und Rechteck sind Vierecker. Die Geometrie dieser Zahlen ist dem Menschen seit Tausenden von Jahren bekannt. Das Thema wird ausdrücklich in dem Buch „Elemente“ des griechischen Mathematikers Euklid behandelt.
Parallelogramm
Parallelogramm kann als die geometrische Figur mit vier Seiten definiert werden, wobei die gegenüberliegenden Seiten parallel zueinander sind. Genauer gesagt ist es ein Viereck mit zwei Paaren paralleler Seiten. Diese parallele Natur verleiht den Parallelogrammen viele geometrische Eigenschaften.
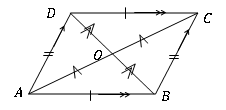
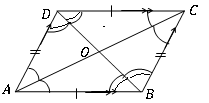
Ein Viereck ist ein Parallelogramm, wenn folgende geometrische Eigenschaften gefunden werden.
• Zwei Paare von gegnerischen Seiten sind gleich lang. (AB = DC, AD = BC)
• Zwei Paare von Gegnerwinkeln sind gleich groß. ([Latex] d \ Hat a b = b \ Hat c d, a \ Hat d c = a \ Hat b c [/latex])
• Wenn die benachbarten Winkel ergänzend sind [Latex] d \ Hat a b + a \ Hat d c = a \ Hat d c + b \ Hat c d = b \ Hat C D + A \ Hat b c = a \ Hat b c + d \ Hat a b = 180^\ circ = \ pi rad [/latex]
• Ein Paar Seiten, die sich gegenseitig gegenseitig widersprechen, ist parallel und gleich lang. (AB = DC & AB∥DC)
• Die Diagonalen halbieren sich gegenseitig (ao = oc, bo = od)
• Jede diagonale teilt das Viereck in zwei kongruente Dreiecke. (∆ADB ≡ ∆BCD, ∆ABC ≡ ∆ADC)
Ferner ist die Summe der Quadrate der Seiten gleich der Summe der Quadrate der Diagonalen. Dies wird manchmal als die bezeichnet Parallelogrammgesetz und hat weit verbreitete Anwendungen in Physik und Technik. (Ab2 + BC2 + CD2 + Da2 = AC2 + Bd2)
Jedes der oben genannten Eigenschaften kann als Eigenschaften verwendet werden, sobald festgestellt wurde, dass das Viereck ein Parallelogramm ist.
Die Fläche des Parallelogramms kann durch das Produkt der Länge einer Seite und der Höhe auf die gegenüberliegende Seite berechnet werden. Daher kann der Bereich des Parallelogramms als angegeben werden
Fläche von Parallelogramm = Basis × Höhe = Ab×H
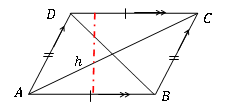
Der Bereich des Parallelogramms ist unabhängig von der Form des individuellen Parallelogramms. Es hängt nur von der Basislänge und der senkrechten Höhe ab.
Wenn die Seiten eines Parallelogramms durch zwei Vektoren dargestellt werden können, kann die Fläche durch die Größe des Vektorprodukts (Kreuzprodukt) der beiden benachbarten Vektoren erhalten werden.
Wenn die Seiten AB und AD durch die Vektoren ([Latex] \ Overrightarrow ab [/latex]) und ([laTex] \ Overrightarrow ad [/latex]) dargestellt werden, ist der Bereich des Parallelogramms durch [[ latex] \ links | \ Overrightarrow ab \ Times \ OverRightarrow ad \ right | = Ab \ cdot ad \ sin \ alpha [/latex], wobei α der Winkel zwischen [Latex] \ Overrightarrow ab [/latex] und [latex] \ Overrightarrow ad [/latex] ist, ist der Winkel.
Im Folgenden finden Sie einige fortgeschrittene Eigenschaften des Parallelogramms;
• Der Bereich eines Parallelogramms ist doppelt so hoch wie ein Dreieck, das von einer seiner Diagonalen erzeugt wird.
• Der Bereich des Parallelogramms wird durch jede Linie, die durch den Mittelpunkt verläuft, in zwei Hälften aufgeteilt.
• Jede nicht enterne affine Transformation führt ein Parallelogramm in ein anderes Parallelogramm
• Ein Parallelogramm hat eine Rotationssymmetrie der Ordnung 2
• Die Summe der Entfernungen von einem Innenraum eines Parallelogramms zu den Seiten ist unabhängig vom Ort des Punktes
Rechteck
Ein Viereck mit vier rechten Winkeln ist als Rechteck bekannt. Es ist ein Sonderfall des Parallelogramms, in dem die Winkel zwischen zwei beliebigen benachbarten Seiten rechtswinkel sind.
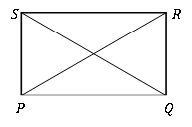
Zusätzlich zu allen Eigenschaften eines Parallelogramms können zusätzliche Eigenschaften erkannt werden, wenn die Geometrie des Rechtecks berücksichtigt wird.
• Jeder Winkel an den Eckpunkten ist ein rechter Winkel.
• Die Diagonalen sind gleich in der Länge und sie halbieren sich gegenseitig. Daher sind die halbierten Abschnitte ebenfalls gleich lang.
• Die Länge der Diagonalen kann mit dem Theorem von Pythagoras berechnet werden:
Pq2 + Ps2 = Sq2
• Die Flächenformel reduziert sich auf das Produkt von Länge und Breite.
Bereich des Rechtecks = Länge × Breite
• Viele symmetrische Eigenschaften befinden sich auf einem Rechteck, wie z. B.;
- Ein Rechteck ist zyklisch, wobei alle Scheitelpunkte am Umfang eines Kreises platziert werden können.
- Es ist äquiangular, wo alle Winkel gleich sind.
- Es ist isogonal, wo alle Ecken innerhalb derselben Symmetrie -Umlaufbahn liegen.
- Es hat sowohl Reflexionssymmetrie als auch Rotationssymmetrie.
Rhombus
Ein Viereck mit allen Seiten ist gleich lang als Rhombus bekannt. Es wird auch als als benannt Gleichseitige Viereck. Es wird angenommen, dass es eine Diamantform hat, ähnlich wie in den Spielkarten.
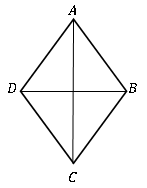
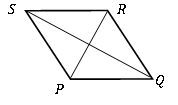
Rhombus ist auch ein Sonderfall des Parallelogramms. Es kann als Parallelogramm mit allen vier Seiten gleich betrachtet werden. Und es gibt neben den Eigenschaften eines Parallelogramms spezielle Eigenschaften, zusätzlich zu den Eigenschaften.
• die Diagonalen der Rhombus nach rechts nach Brisekten; Diagonale sind senkrecht.
• Die Diagonalen halbieren die beiden gegenüberliegenden inneren Winkel.
• Mindestens zwei der angrenzenden Seiten sind gleich lang.
Die Fläche des Rhombus kann in derselben Methode wie das Parallelogramm berechnet werden.
Was ist der Unterschied zwischen Rhombus und Rechteck?
• Rhombus und Rechteck sind Vierecker. Rechteck und Rhombus sind besondere Fälle der Parallelogramme.
• Die Fläche einer beliebigen kann mit der Formel berechnet werden Basis × Höhe.
• Berücksichtigung der Diagonalen;
- Die Diagonalen der Rhombus nach rechts nach Basiten, und die gebildeten Dreiecke sind gleichseitig.
- Die Diagonalen des Rechtecks sind gleich lang und halbieren sich gegenseitig. halbierende Abschnitte sind gleich lang. Die Diagonalen halbieren das Rechteck in zwei kongruente rechte Dreiecke.
• Berücksichtigung der inneren Winkel;
- Die inneren Winkel des Rhombus werden von den Diagonalen halbiert
- Alle vier inneren Winkel des Rechtecks sind rechte Winkel.
• Berücksichtigung der Seiten;
- Da alle vier Seiten im Rhombus gleich sind, ist das vierfache Quadrat einer Seite gleich der Summe der Quadrate der Diagonale (unter Verwendung des Parallelogrammgesetzes)
- In Rechtecken ist die Summe der Quadrate der beiden benachbarten Seiten gleich dem Quadrat der Diagonale an den Enden. (Pythagoras -Regel)


