Unterschied zwischen kongruent und gleich

Kongruent gegen gleich

Kongruent und gleich sind ähnliche Konzepte in der Geometrie, aber oft missbraucht und verwirrt.

Gleich

Gleichberechtigt bedeutet, dass die Größen oder Größen von zwei im Vergleich gleich sind. Das Konzept der Gleichheit ist ein bekanntes Konzept in unserem täglichen Leben. Als mathematisches Konzept muss es jedoch mit strengeren Maßnahmen definiert werden. Verschiedenes Feld verwendet eine andere Definition für die Gleichheit. In der mathematischen Logik wird es unter Verwendung von Paenos Axiomen definiert. Gleichheit bezieht sich auf die Zahlen; oft Zahlen, die Eigenschaften darstellen.

Im Kontext der Geometrie hat die Gleichheit die gleichen Auswirkungen wie bei der gemeinsamen Verwendung des Begriffs gleich. Es heißt, wenn die Attribute von zwei geometrischen Figuren gleich sind, sind die beiden Figuren gleich. Zum Beispiel kann die Fläche eines Dreiecks der Fläche eines Quadrats gleich sein. Hier geht es nur um die Größe des Eigentums "Bereich" und sie sind gleich. Aber die Zahlen selbst können nicht als dasselbe angesehen werden. 

Kongruent

Im Kontext der Geometrie bedeutet kongruent in beiden Figuren (Form) und Größen gleich. Oder in einfacheren Worten, wenn man als exakte Kopie der anderen betrachtet werden kann, sind die Objekte unabhängig von der Positionierung kongruent. Es ist das äquivalente Konzept der Gleichheit in der Geometrie. Im Fall der Kongruenz sind auch viele strengere Definitionen in der analytischen Geometrie bereitgestellt. 

Unabhängig von der Orientierung der Dreiecke, die oben zeigen, können sie so positioniert werden, dass sie sich perfekt überlappen. Daher sind sie sowohl in Größe als auch in Form gleich gleich. Daher sind sie kongruente Dreiecke. Eine Figur und ihr Spiegelbild sind ebenfalls kongruent. (Sie können überlappt werden, nachdem sie sie um eine Achse in der Ebene der Form drehen.). 

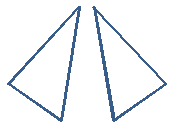
Auch wenn die Figuren Spiegelbilder sind, sind sie kongruent.

Die Kongruenz in Dreiecken ist wichtig für das Studium der Ebenengeometrie. Damit zwei Dreiecke kongruent sind, sollen die entsprechenden Winkel und die Seiten gleich sein. Dreiecke können kongruent angesehen werden, wenn die folgenden Bedingungen erfüllt sind.

• SSS (Seitenseite)  Wenn alle drei entsprechenden Seiten gleich lang sind.

• SAS (Seitenwinkelseite)  Ein Paar entsprechender Seiten und der enthaltene Winkel sind gleich.

• ASA (Winkelseitenwinkel)  Ein Paar entsprechender Winkel und die mitgelieferte Seite sind gleich.

• AAS (Winkelwinkelseite)  Ein Paar entsprechender Winkel und eine nicht eingelegte Seite sind gleich.

• HS (Hypotenuse -Bein eines rechten Dreiecks)  Zwei rechte Dreiecke sind kongruent, wenn die Hypotenuse und eine Seite gleich sind.

Der Fall AAA (Winkelwinkelwinkel) ist kein Fall, in dem die Kongruenz immer gültig ist. Zum Beispiel haben die folgenden zwei Dreiecke gleiche Winkel, aber nicht kongruent, da die Größen der Seiten unterschiedlich sind. 

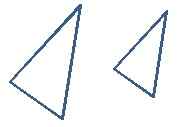
Was ist der Unterschied zwischen Kongruent und Gleicher?

• Wenn einige Attribute geometrischer Figuren in großer Größe gleich sind, dann wird bezeichnet, dass sie gleich sind.

• Wenn sowohl die Größen als auch die Zahlen gleich sind, sollen die Zahlen kongruent sein.

• Gleichheit betrifft die Größe (Zahlen), während die Kongruenz sowohl die Form als auch die Größe einer Figur betrifft.