Unterschied zwischen Parabola und Hyperbel
Parabola gegen Hyperbel
Kepler beschrieb die Umlaufbahnen von Planeten als Ellipsen, die später von Newton modifiziert wurden, als er zeigte. Es gibt viele Ähnlichkeiten zwischen einer Parabola und einer Hyperbola, aber es gibt auch Unterschiede, da es verschiedene Gleichungen gibt, um geometrische Probleme zu lösen. Um die Unterschiede zwischen einer Parabel und einer Hyperbel besser zu verstehen, müssen wir diese konischen Abschnitte verstehen.

Bild mit freundlicher Genehmigung: http: // cseligman.com
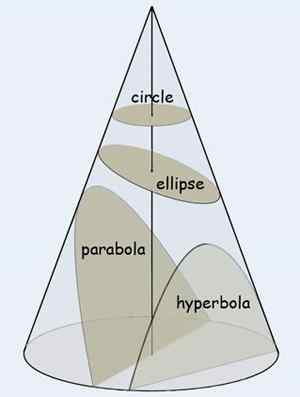
Ein Abschnitt ist eine Oberfläche oder der Umriss dieser Oberfläche, das durch Schneiden einer festen Figur mit einer Ebene gebildet wird. Wenn die feste Figur ein Kegel ist, wird die resultierende Kurve als Kegelabschnitt bezeichnet. Die Art und Form des Kegelabschnitts wird durch den Schnittwinkel der Ebene und die Achse des Kegels bestimmt. Wenn der Kegel im rechten Winkel zur Achse geschnitten wird, erhalten wir eine kreisförmige Form. Wenn Sie mit weniger als einem rechten Winkel geschnitten sind, aber mehr als der an der Seite des Kegels hergestellte Winkel führt zu einer Ellipse. Wenn die Kurve parallel zur Seite des Kegels geschnitten ist, ist die erhalten. Wie Sie aus den Figuren sehen können, sind Kreise und Ellipsen geschlossene Kurven, während Parabolas und Hyperbolen offene Kurven sind. Bei einer Parabel werden die beiden Arme schließlich parallel zueinander, während es bei einer Hyperbel nicht so ist.
Da Kreise und Parabel gebildet werden, indem ein Kegel in bestimmten Winkeln geschnitten wird, sind alle Kreise identisch und alle Parabolas sind identisch in Form. Im Fall von Hyperbolas und Ellipsen gibt es einen weiten Winkeln zwischen der Ebene und der Achse, weshalb sie dazu neigen, eine breite Palette von Formen zu haben. Die Gleichungen der vier Arten von Kegelabschnitten sind wie folgt.
Kreis x2+y2= 1
Ellipse x2/A2+ y2/B2= 1
Parabola-y2= 4AX
Hyperbel2/A2- y2/B2= 1


