Unterschied zwischen Punktgruppe und Raumgruppe
Schlüsselunterschied - Punktgruppe vs Raum Gruppe
Die Begriffe Punktgruppe und Raumgruppe werden in der Kristallographie verwendet. Die Kristallographie ist die Untersuchung der Anordnung von Atomen in einem kristallinen Feststoff. Die kristallographische Punktgruppe ist eine Reihe von Symmetrieoperationen, die mindestens einen Punkt unmacht lassen. Eine Symmetrieoperation ist ein Akt, um das Originalbild eines Objekts auch nach dem Bewegen zu erhalten. Die in Punktgruppen verwendeten Symmetrieoperationen sind Rotationen und Reflexionen. Eine Raumgruppe ist die 3D -Symmetriegruppe einer Konfiguration im Raum. Eine Symmetriegruppe ist die Gruppe aller Transformationen, die ohne Variation der Zusammensetzung während des Gruppenvorgangs erhalten wurden. Der Schlüsselunterschied Zwischen Punktgruppe und Raumgruppe ist das Es gibt 32 kristallographische Punktgruppen, während es 230 Weltraumgruppen gibt, die durch die Kombination von 32 Punkte und 14 Bravais -Gitter erzeugt werden.
INHALT
1. Überblick und wichtiger Unterschied
2. Was ist die Punktgruppe
3. Was ist Raumgruppe
4. Seite für Seitenvergleich - Punktgruppe gegen Raumgruppe in tabellarischer Form
5. Zusammenfassung
Was ist die Punktgruppe?
Die kristallographische Punktgruppe ist eine Reihe von Symmetrieoperationen, die mindestens einen Punkt unmacht lassen. Die in Punktgruppen beschriebenen Symmetrieoperationen sind Rotationen und Reflexionen. In der Point Group -Symmetrieoperationen wird ein zentraler Punkt im Objekt unberührt (fix. Dort sollten die makroskopischen Merkmale des Objekts vor und nach dem Symmetrievorgang gleich bleiben.
Für ein bestimmtes Objekt besteht eine bestimmte Anzahl von Symmetrieoperationen möglich (mit definierten geometrischen Beziehungen zwischen Symmetrieoperationen). Das Objekt soll die von der Punktgruppe beschriebene Symmetrie beschreiben lassen. Daher werden verschiedene Objekte mit unterschiedlichen Punktsymmetrien von verschiedenen Punktgruppen beschrieben.
In der Notation von Punktgruppen werden zwei Systeme verwendet;
-
Schoenflies Notation
In Schoenflies Notationssystem werden Punktgruppen als C bezeichnetnv, CNH, DNH, TD, ÖH, usw. Die verschiedenen in diesem Notationssystem verwendeten Symbole sind unten angegeben.
- n ist die höchste Anzahl von Rotationsachsen
- V ist die vertikale Spiegelebene (nur dann erwähnt, wenn keine horizontalen Spiegelebenen vorhanden sind)
- H sind die horizontalen Spiegelebenen
- T ist eine tetraedrische Punktgruppe
- ist eine oktaedrische Punktgruppe
Zum Beispiel cN wird verwendet. Wenn es als c angegeben wirdNH, es bedeutet, dass es ein c gibtN zusammen mit einer Spiegelebene (Reflexionsebene) senkrecht zur Rotationsachse. Im Gegensatz dazu cnv ist cN mit einer Spiegelebene parallel zur Rotationsachse. Wenn die Punktgruppe als s angegeben ist2n, Es zeigt an, dass die Punktgruppe nur eine 2n-fache Rotationsreflexionsachse hat.
-
Hermann-Mauguin Notation
Das Hermann-Mauguin-Notationssystem wird üblicherweise für Raumgruppen verwendet. Es wird aber auch für kristallographische Punktgruppen verwendet. Es gibt die höchste Rotationsachse. Zum Beispiel wird die Punktgruppe mit nur einer 2-fachen Rotationsachse als 2 bezeichnet. Die Punktgruppe als c angegeben2H von schoenflies Notation wird als 2/m im Hermann-Mauguin-Notationssystem angegeben, in dem das Symbol 'm' eine Spiegelebene angibt und das Slash-Symbol angibt, dass die Spiegelebene senkrecht zur zweifachen Achse ist. Die folgende Tabelle zeigt verschiedene Notationen von Punktgruppen für verschiedene Gittersysteme.
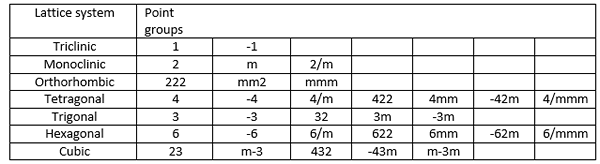

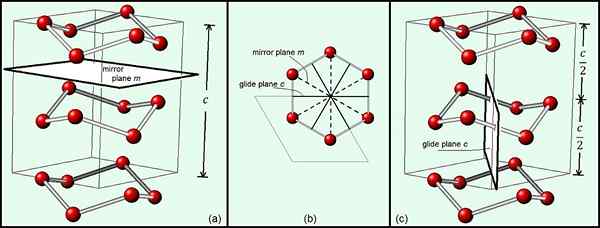
Abbildung 01: Die Spiegelebenen und Gleitebenen mit hexagonalem Eis zeigen, dass die Raumgruppe von Eis p63/mmc ist
Es gibt 32 Punktegruppen. Die einfachsten Punktgruppen sind 1, 2, 3, 4, 5 und 6. Alle diese Punktgruppen umfassen nur eine Rotationsachse. Für Rotary -Inversionen gibt es Achsen mit dem Namen -1, m, -3, -4 und -6. Andere 22 -Punkte -Gruppen sind Kombinationen dieser Punktgruppen.
Was ist Raumgruppe?
Eine Raumgruppe ist die 3D -Symmetriegruppe einer Konfiguration im Raum. Es gibt 230 Weltraumgruppen. Diese 230 Gruppen sind eine Kombination aus 32 kristallographischen Punktgruppen (oben erwähnt) und 14 Bravais -Gitter. Der Bravais -Gitter sind in der folgenden Tabelle angegeben.
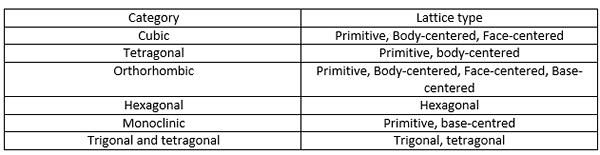
Eine Raumgruppe gibt eine Beschreibung der Symmetrie eines Kristalls an. Weltraumgruppen sind Kombinationen der Translationssymmetrie von Einheitenzellen- und Symmetrieoperationen wie Rotation, Rotationsinversion, Reflexion, Schraubenachse und Symmetrieoperationen der Gleitebene.
Was ist der Unterschied zwischen Punktgruppe und Raumgruppe?
Point Group vs Space Group | |
| Die kristallographische Punktgruppe ist eine Reihe von Symmetrieoperationen, die mindestens einen Punkt unmacht lassen. | Eine Raumgruppe ist die 3D -Symmetriegruppe einer Konfiguration im Raum. |
| Komponenten | |
| Es gibt 32 kristallographische Punktgruppen. | Es gibt 230 Weltraumgruppen (erzeugt durch die Kombination von 32 -Punkte -Gruppen und 14 Bravais -Gitter). |
| Symmetrieoperationen | |
| Die bei der Punktgruppenerkennung verwendeten Symmetrieoperationen sind Rotation und Reflexion. | Die bei der Erkennung von Raumgruppen verwendeten Symmetrieoperationen sind Dreh-, Rotationsinversions-, Reflexions-, Schraubenachse- und Gleitebene-Symmetrieoperationen. |
Zusammenfassung - Punktgruppe vs Raum Gruppe
Punktgruppen und Weltraumgruppen sind Begriffe, die unter der Kristallographie beschrieben werden. Die kristallographische Punktgruppe ist ein Satz von Symmetrieoperationen, die alle mindestens einen Punkt unmacht lassen. Eine Raumgruppe ist die 3D -Symmetriegruppe einer Konfiguration im Raum. Der Unterschied zwischen Punktgruppe und Raumgruppe besteht darin, dass es 32 kristallographische Punktgruppen gibt, während es 230 Weltraumgruppen gibt (erzeugt durch die Kombination von 32 Punktengruppen und 14 Bravais -Gitter).
Referenz:
1.„2: Symmetrieoperationen und Symmetrieelemente.”Chemistry Libretexte, Libretexte, 6. Mai 2017. Hier verfügbar
2.„Kristallographische Punktgruppe.”Wikipedia, Wikimedia Foundation, 28. Februar. 2018. Hier verfügbar
Bild mit freundlicher Genehmigung:
1.'ICE IH Space Group'By Dbuckingham42 - eigene Arbeit, (CC BY -SA 4.0) über Commons Wikimedia


