Unterschied zwischen Transponierung und inverser Matrix

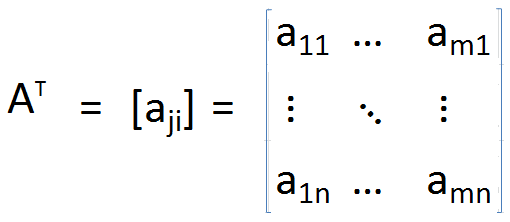
Transponieren gegen inverse Matrix
 

Die Transponierung und die Umkehrung sind zwei Arten von Matrizen mit speziellen Eigenschaften, denen wir in Matrixalgebra begegnen,. Sie unterscheiden.

Sie haben große Anwendungen im Bereich der linearen Algebra und der abgeleiteten Implementierungen wie Informatik.

Mehr über die Transponierungsmatrix

Transponieren einer Matrix A kann als die Matrix identifiziert werden, die durch Umbau von Spalten als Zeilen oder Zeilen als Spalten erhalten wird. Infolgedessen werden die Indizes jedes Elements austauscht. Formell förmlich, um Matrix zu transponieren A, ist definiert als

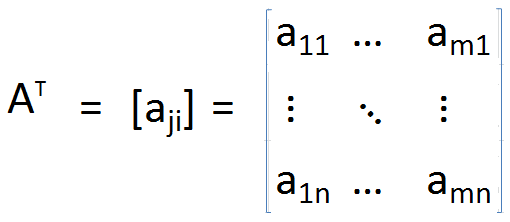
Wo

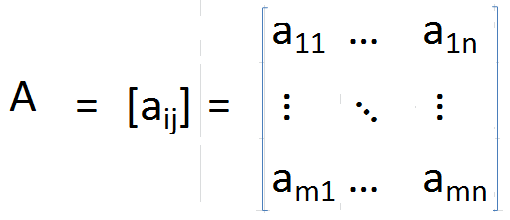
In einer Transponierungsmatrix bleibt die Diagonale unverändert, aber alle anderen Elemente werden um die Diagonale umgedreht. Auch die Größe der Matrizen ändert sich auch von m × n bis n × m.

Die Transponierung hat einige wichtige Eigenschaften, und sie ermöglichen eine leichtere Manipulation von Matrizen. Außerdem werden einige wichtige Transponierungsmatrizen auf der Grundlage ihrer Merkmale definiert. Wenn die Matrix gleich ihrer Transponierung ist, ist die Matrix symmetrisch. Wenn die Matrix gleich ihrer Negativ der Transponierung ist, ist die Matrix ein schief symmetrischer. Die konjugierte Transponierung einer Matrix ist die Transponierung der Matrix durch die Elemente, die durch ihr komplexes Konjugat ersetzt wurden.

Mehr über inverse Matrix

Die Umkehrung einer Matrix wird als eine Matrix definiert, die die Identitätsmatrix beim Zusammenführen ergibt. Daher per Definition, wenn Ab = ba = i Dann B ist die inverse Matrix von A Und A ist die inverse Matrix von B. Also, wenn wir berücksichtigen B = A^-1 , Dann Aa^-1 = A^-1A = i

Damit eine Matrix invertierbar ist, ist der notwendige und ausreichende Zustand, dass die Determinante von A ist nicht Null; ich.e |A| = det (A) ≠ 0. Eine Matrix soll invertierbar, nicht-singular oder nicht degenerativ sein, wenn sie diesen Zustand erfüllt. Es folgt dem A ist eine quadratische Matrix und beide A^-1 Und A hat die gleiche Größe.

Die Umkehrung der Matrix A kann mit vielen Methoden in linearen Algebra wie Gaußschen Eliminierung, Eigenkomposition, Cholesky -Zersetzung und Carmers Regel berechnet werden. Eine Matrix kann auch durch Blockinversionsmethode und Neuman -Serien invertiert werden.

Was ist der Unterschied zwischen der Transponierung und der inversen Matrix?

• Die Transponierung wird erhalten, indem die Säulen und Zeilen in der Matrix neu angeordnet werden, während die Umkehrung durch eine relativ schwierige numerische Berechnung erhalten wird. (Aber in Wirklichkeit sind beide lineare Transformationen)

• In einem direkten Ergebnis ändern die Elemente in der Transponierung nur ihre Position, aber die Werte sind gleich. Aber in der Umkehrung können sich die Zahlen vollständig von der ursprünglichen Matrix unterscheiden.

• Jede Matrix kann eine Transponierung haben, aber das Inverse wird nur für quadratische Matrizen definiert, und die Determinante muss eine Determinante ungleich Null sein.