Unterschied zwischen Integration und Summierung

Integration vs Summe
 

In der obigen High School -Mathematik finden sich in der Integration und Summierung häufig in mathematischen Operationen. Sie werden anscheinend als unterschiedliche Werkzeuge und in verschiedenen Situationen verwendet, aber sie haben eine sehr enge Beziehung.

Mehr über die Summierung

Summierung ist das Hinzufügen einer Abfolge von Zahlen und die Operation wird häufig durch das griechische Kapitalbuchstaben Sigma σ bezeichnet. Es wird verwendet, um die Summierung und gleich der Summe/Gesamtquelle der Sequenz abzukürzen. Sie werden oft verwendet, um die Serie darzustellen, die im Wesentlichen unendliche Sequenzen summiert sind. Sie können auch verwendet werden, um die Summe der Vektoren, Matrizen oder Polynome anzuzeigen.

Die Summierung erfolgt normalerweise für einen Wertebereich, der durch einen allgemeinen Begriff dargestellt werden kann, z. Der Ausgangspunkt und der Endpunkt der Summe werden als untere gebundene bzw. Obergrenze der Summe bezeichnet.

Zum Beispiel die Summe der Sequenz a₁, A₂, A₃, A₄, … , A_N ist ein₁ + A₂ + A₃ +… + A_N Dies kann leicht unter Verwendung der Summierungsnotation als ∑ dargestellt werden^N_{I = 1} A_ich; Ich wird als Index der Summierung bezeichnet.

Viele Variationen werden für die Summation basierend auf der Anwendung verwendet. In einigen Fällen kann die Obergrenze und die Untergrenze als Intervall oder Bereich angegeben werden, wie z. B. ∑_{1 ≤ i ≤ 100} A_ich und ∑_{i∈ [1,100]} A_ich. Oder es kann als eine Reihe von Zahlen wie ∑ angegeben werden_i∈P A_ich , wobei P ein definierter Satz ist.

In einigen Fällen können zwei oder mehr Sigma -Zeichen verwendet werden, können jedoch wie folgt verallgemeinert werden. ∑_J ∑_k A_jk = ∑_{J, k} A_jk.

Außerdem folgt die Summierung viele algebraische Regeln. Da die eingebettete Operation die Zugabe ist, können viele der gemeinsamen Algebra -Regeln auf die Summen selbst und für die individuellen Begriffe angewendet werden, die durch die Summierung dargestellt sind.

Mehr über die Integration

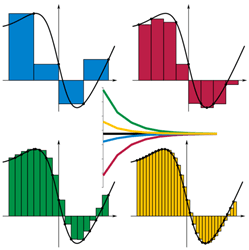
Die Integration ist definiert als der umgekehrte Differenzierungsprozess. In seiner geometrischen Sicht kann es aber auch als der Bereich betrachtet werden, der durch die Kurve der Funktion und die Achse eingeschlossen ist. Die Berechnung der Fläche ergibt daher den Wert eines bestimmten Integrals, wie im Diagramm gezeigt.

Bildquelle: http: // en.Wikipedia.org/wiki/Datei: riemann_sum_convergence.png

Der Wert des definitiven Integrals ist tatsächlich die Summe der kleinen Streifen innerhalb der Kurve und der Achse. Die Fläche jedes Streifen. Breite ist ein Wert, den wir wählen können, z. B. ∆x. Und die Höhe ist ungefähr der Wert der Funktion am betrachteten Punkt, beispielsweise F(X_ich). Aus dem Diagramm aus ist es offensichtlich, dass die Streifen, je kleiner die Streifen sind.

Also im Allgemeinen das eindeutige Integral ICH, zwischen den Punkten A und B (ich.e im Intervall [a, b] wo aICH ≅ F(X₁) ∆x + F(X₂) ∆x + ⋯ + F(X_N) ∆x, wobei n die Anzahl der Streifen ist (n = (b-a)/∆x). Diese Summe des Bereichs kann leicht unter Verwendung der Summationsnotation als dargestellt werden ICH ≅ ∑^N_{I = 1} F(X_ich) ∆x. Da die Näherung besser ist, wenn ∆x kleiner ist, können wir den Wert berechnen, wenn ∆x → 0. Daher ist es vernünftig zu sagen ICH = lim_{∆x → 0} ∑^N_{I = 1} F(X_ich) ∆x.

Als Verallgemeinerung aus dem obigen Konzept können wir den ∆x basierend auf dem von I indizierten betrachteten Intervall auswählen (die Breite des Bereichs basierend auf der Position). Dann bekommen wir

ICH= lim_{∆x → 0} ∑^N_{I = 1} F(X_ich) ∆x_ich = _A∫^B F(x) dx

Dies ist als Reimann -Integral der Funktion bekannt F(x) im Intervall [a, b]. In diesem Fall sind A und B als Obergrenze und Untergrenze des Integrals bekannt. Reimann Integral ist eine grundlegende Form aller Integrationsmethoden.

Im Wesentlichen ist die Integration die Summierung des Bereichs, wenn die Breite des Rechtecks ​​infinitesimal ist.

Was ist der Unterschied zwischen Integration und Summierung?

• Summierung addiert eine Abfolge von Zahlen. Normalerweise ist die Summierung in dieser Form ∑ angegeben. ∑^N_{I = 1} A_ich Wenn die Begriffe in der Sequenz ein Muster haben und mit einem allgemeinen Begriff ausgedrückt werden können.

• Die Integration ist im Grunde die Fläche, die durch die Kurve der Funktion, die Achse sowie die oberen und unteren Grenzen begrenzt wird. Dieser Bereich kann als Summe viel kleinerer Bereiche im begrenzten Bereich angegeben werden.

• Summierung umfasst die diskreten Werte mit den oberen und unteren Grenzen, während die Integration kontinuierliche Werte beinhaltet.

• Integration kann als besondere Form der Summierung interpretiert werden.

• In numerischen Berechnungsmethoden wird immer die Integration als Summe durchgeführt.